
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЭКОНОМИКО-СТАТИСТИЧЕСКИЙ АНАЛИЗ УРАВНЕНИЙ РЕГРЕССИИЭкономико-статистический анализ корреляционно-регрессионной модели на адекватность реальным условиям включает в себя математическую проверку: 1) целесообразности включения выбранных факторов в модель (уравнение) регрессии; 2) правомерности распространения свойств модели, полученных по данным выборок, на генеральную совокупность. Проверка целесообразности включения каждого фактора в модель осуществляется по данным шаговой регрессии. О значимости введенного фактора можно судить по изменениям коэффициента множественной корреляций
где
Таким образом, Если на анализируемом шаге регрессии произошло увеличение коэффициента множественной корреляции и уменьшение Более строгую оценку полезности для уравнения введенного фактора дает сравнение расчетного F-значения для дисперсионного анализа с табличным  где
Если то влияние включенных в уравнение регрессии факторов на функцию весьма достоверно. В рассматриваемом примере при
Таблица 7 – Анализ факторов корреляционно-регрессионных уравнений по значению F для дисперсионного анализа
Анализ таблицы 7 показывает правомерность включения по имеющимся исходным данным выборок и переменной Широко известным критерием оценки качества полученного уравнения регрессии (по имеющимся данным выборок) является средний коэффициент (ошибка) аппроксимации:
Ее допустимая величина колеблется в пределах 12 – 15 % [18, с. 44]. В рассматриваемом примере для линейного уравнения Наконец, в качестве одного из критериев правильности полученного уравнения регрессии можно использовать отношение среднеквадратического отклонения от регрессии
В рассматриваемое примере имеем: для линейного уравнения: для нелинейного уравнения: Очевидно, предпочтительнее взять лилейное уравнение. Заметим, что двумя последними критериями в соответствии с используемыми программами можно пользоваться на последнем шаге регрессии. Если по результатам предшествующего экономико-статистического анализа будет целесообразно выбрать не окончательное, а промежуточное уравнение регрессии, следует весь расчет повторить сначала, отбросить незначащие факторы и уже для выбранного уравнения выполнить дополнительную проверку по формулам (39), (40). Выполненный анализ обоих уравнений по изменению множественного коэффициента корреляции 1) выбрать в качестве уравнения регрессии, наиболее адекватного исследуемому процессу влияния субъективных факторов производительности труда на и изменение процентов выполнения норм выработки станочников механического цеха, линейное уравнение:
2) признать его полную адекватность имеющимся данным исходных выборок. Выполним теперь проверку правомерности распространения найденного уравнения регрессии на генеральную совокупность, т.е. проверку правомерности его практического использования. В качестве такого критерия можно использовать проверку значимости коэффициентов полученного уравнения регрессии по Т-значению:
где Если то проверяемый коэффициент регрессии является значимым. Значения Несоблюдение неравенства (42) при наличии предварительно установленной по критерию Стьюдента надежности соответствующего коэффициента парной или частной корреляции говорит о нелинейности связи между функцией и рассматриваемым аргументом. В данном примере примем наиболее употребительный уровень значимости 0,05 (таблица 8).
Таблица 8 – Анализ значимости коэффициентов регрессии в уравнениях шаговой регрессий
Данные таблицы 8 по нелинейному уравнению подтверждают установленную ранее нелинейную связь между При исследовании адекватности уравнения регрессии нельзя забывать о таком явлении, как автокорреляция. Под автокорреляцией понимается корреляция между членами одного и того же динамического ряда. Ее наличие в исходных данных приводит к низкой надежности получаемого уравнения регрессии. Существует ряд методов обнаружения автокорреляции. Наиболее простым и достаточно обоснованным является метод, предложенный Дарбином и Уотсоном. Был сконструирован критерий, связанный с гипотезой о существовании автокорреляции первого порядка, т.е. автокорреляции между соседними членами ряда, составленного из разностей фактических и расчетных (по уравнению регрессии) значений функции
где Коэффициент Для
 ; ;
автокорреляция отрицательна, если автокорреляция отсутствует, если Если величина расчетной
Таблица 9 – Значения критерия Дарбина - Уотсона при уровне значимости 0,05 [14, с, 160]
В рассматриваемом примере для линейного уравнения регрессии оценка первого нециклического коэффициента автокорреляции Расчетное значение 1,63 < 2,314 < 4 -1,63 или 1,63 < 2,314 < 2,37. Следовательно, автокорреляция исходных данных отсутствует. Таким образом, окончательная экономико-математическая модель зависимости процентов выполнения норм выработки станочников механического цеха
Статистическая наука выработала несколько методов исключения автокорреляции: 1) метод Фриша - Boy, 2) метод последовательных разностей, 3) метод авторегрессионных преобразований. Согласно методу Фриша - Boy в уравнение регрессии вводится время в качестве дополнительного фактора. Тогда уравнения регрессии (30) и (31) принимают вид: линейные: степенные: В соответствии с этим методом при обнаружении автокорреляции в модель (в уравнение регрессии) вводят еще одну переменную – время Наиболее сложным этапом, завершающим корреляционно-регрессионное моделирование, является интерпретация уравнения, т.е. перевод его с языка статистики и математики на язык экономиста. Интерпретация [18, c. 44] начинается с выяснения того, как каждый аргумент влияет на функцию. Характеристикой этого влияния является соответствующий коэффициент регрессии В рассматриваемом уравнении (46) коэффициенты регрессий при показателях законченное образование Далее необходимо определить силу и долю влияния на функцию каждого из вошедших в модель аргументов. Силу влияния каждого аргумента на функцию можно найти о помощью где
Так как в уравнении (49) вcе переменные выражены в одних единицах измерения, то В рассматриваемом уравнении (46) Для определения доли влияния аргументов на функцию находятся произведения парных коэффициентов корреляции функции с каждым аргументом Дм уравнения (46 ) данный расчет представлен в таблице 10.
Таблица 10 – Определение доли влияния каждого фактора на функцию по уравнению (46)
Почти 80 % общей вариации процентов выполнения норм выработки станочников вызвано изменением общего стажа их работы и только 20 % – законченным образованием (разумеется, из числа учтенных факторов). Уравнение регрессии позволяет прогнозировать значения функции Для решения поставленной задачи можно воспользоваться коэффициентами эластичности:
где
В рассматриваемом уравнении коэффициенты эластичности (см. приложение 4)
Прогнозируя функцию по рассчитанному уравнению регрессии, естественно полагать, что фактические ее значения не будут совпадать с расчетными, так как уравнение регрессии описывает связь лишь в общем, в среднем. Поэтому важным и завершающим моментом интерпретации уравнения регрессии является установление надежности получаемых по нему прогнозных решений. Мерой надежности в линейной регрессии является среднее квадратическое отклонение от регрессии, которое характеризует степень рассеяния фактических значений функции от расчетных
Доверительный интервал, в котором с заданной вероятностью будет заключаться расчетное значение функции в генеральной совокупности, определяется так:
где Уровень значимости принимается обычно 0,05. Он соответствует 95 %-ному уровню надежности. В рассматриваемом уравнении (46)
Полученный интервал означает: с вероятностью, равной 0,95 (т.е. в 95 случаях из 100) можно утверждать, что фактические значения функции будут находиться в границах:
или в общем случае
Возьмем какого-либо станочника механического цеха из числа вошедших в выборку, например, Шанина С. В. (таблица 1, № 31). Его законченное образование 8 классов, общий стаж работы 14 лет. По найденному уравнению связи определяем вероятный, процент выполнения им нормы выработки:
Эта величина представляет собой наилучшее возможное в рамках модели приближение к действительности. Однако нельзя утверждать, что это реальный процент выполнения рабочим Шаниным С.В. его нормы выработки. Зато с большой уверенностью можно назвать интервал, в котором заключен его фактический процент выполнения. При вероятности 0,95 границы доверительного интервала для Шанина С.В. составят:
или Фактический процент выполнения норм выработки Шанина С.В. (175 %) действительно лежит в этом интервале. При меньшей надежности – 0,8 (т.е. в 80 случаях из 100) границы доверительного интервала сужаются до
Заметим, что в случае нелинейной регрессии доверительные границы носят приближенный характер. Уравнение регрессии позволяет проводить прогноз функции двоякого рода: интерполяцию и экстраполяцию. В первом случае значения независимых факторов-аргументов лежат в пределах исходной совокупности и надежность результата определяется указанными ранее оценками: среднеквадратическим отклонением от регрессии, При экстраполяции значения независимых факторов-аргументов находятся вне исходной выборки, поэтому к результатам следует подходить с осторожностью. В рассматриваемом примере это может быть прогноз выработки рабочего 5-го – 6-го разрядов (в исходной совокупности 3-го – 4-го разрядов), Особенно осторожно следует экстраполировать во времени, когда исходные данные берутся за разные периоды времени. Для обеспечения надежности экстраполяции необходимо соблюдение трех условий [28, с. 287 - 288]: 1) надежность и представительность исходных данных не должна вызывать сомнений; 2) возможность экстраполяции должна подтверждаться качественным анализом; 3) результатом экстраполяции должно быть не получение точной величины функции, а определение ее доверительного интервала. Многое зависит и от "удаления" значений факторов-аргументов прогнозируемого наблюдения от исходной выборки. Если выход за рамки диапазона наблюдений незначительный, то и погрешность результата, связанная с этим, будет незначительной и с лихвой охватится ее доверительным интервалом. Чем дальше выходит прогноз за пределы наблюдений, чем выше риск получения ошибочной оценки. И все-таки в условиях отсутствия другой информации даже такие регрессии практически полезны. Областью широкого применения регрессии в прогнозировании служат статистика качества продукции [27], прогноз производительности труда [3, 4, 7, 8, 17, 25, 31], себестоимости продукции [7, 21, 27, 29, 34], спроса на продукцию [2, 17], ритмичности производства, заработной платы [34] и т.п. Корреляционно-регрессионное моделирование используется для выбора экономических показателей [32]. В последние годы широкое развитие корреляционно-регрессионное моделирование получает в определении различных плановых нормативов: норм времени, трудоемкости, численности работающих различных категорий, длительности производственных циклов изготовления изделий, материалоемкости продукции, комплексных расходов в себестоимости продукции и т.д. Занимаясь тем или иным прикладным вопросом корреляционно-регрессионного моделирования, студент должен самостоятельно или с помощью своего научного руководителя подобрать необходимую литературу по теме исследования, взяв указанные в данном разделе работы за отправной момент поиска. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 325. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 и среднеквадратического отклонения от регрессии
и среднеквадратического отклонения от регрессии  :
: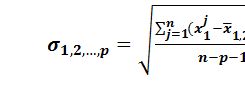 , (35)
, (35) – фактическое значение функции в j-м наблюдении;
– фактическое значение функции в j-м наблюдении; – значение функции, рассчитанное по уравнению регрессии для фактических значений
– значение функции, рассчитанное по уравнению регрессии для фактических значений  в j-м наблюдении.
в j-м наблюдении. на втором шаге привело к росту
на втором шаге привело к росту  на 12,5 % и увеличению точности оценок
на 12,5 % и увеличению точности оценок  на 5,8 %. В нелинейной регрессии повышение точности
на 5,8 %. В нелинейной регрессии повышение точности  составило 1,6 %. Следовательно, введение
составило 1,6 %. Следовательно, введение  , приведенным в приложении 8 при
, приведенным в приложении 8 при  и
и  степенях свободы. В F-значении находит отражение среднеквадратичное отклонение от регрессии:
степенях свободы. В F-значении находит отражение среднеквадратичное отклонение от регрессии: , (36)
, (36)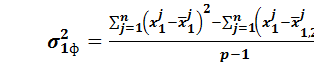 . (37)
. (37) , (38)
, (38) = 2и
= 2и 

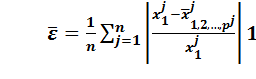 . (39)
. (39) 
 = 7,3 %, для нелинейного
= 7,3 %, для нелинейного  . В случае хорошего согласия уравнения с исходами данными это отношение должно стремиться к единице, т.е.
. В случае хорошего согласия уравнения с исходами данными это отношение должно стремиться к единице, т.е. (40)
(40) ;
;  .
. 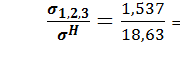
 , F-значению и, наконец, по
, F-значению и, наконец, по 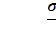 позволяет:
позволяет: ;
; , (41)
, (41) – стандартная (среднеквадратическая) ошибка коэффициента регрессии при i-й переменной, i = 2, 3, …, р.
– стандартная (среднеквадратическая) ошибка коэффициента регрессии при i-й переменной, i = 2, 3, …, р. , (42)
, (42) степенях свободы и различном уровне значимости.
степенях свободы и различном уровне значимости.

 (1,89 < 2,02). Но степень нелинейности невелика, так как по линейному уравнению
(1,89 < 2,02). Но степень нелинейности невелика, так как по линейному уравнению  . В линейном уравнении все коэффициенты значимы, следовательно, его можно с полной уверенностью применять на практике.
. В линейном уравнении все коэффициенты значимы, следовательно, его можно с полной уверенностью применять на практике. . Соответствующая критерию Дарбина - Уотсона статистика
. Соответствующая критерию Дарбина - Уотсона статистика  (отношение Дарбина) имеет вид:
(отношение Дарбина) имеет вид: , (43)
, (43) . (44)
. (44)  называется первым нециклическим коэффициентом автокорреляции. Если автокорреляция отсутствует, он равен 0. Если же наблюдается полная автокорреляция, то он равен +1 или -1. Отсюда следует, что при отсутствии автокорреляции
называется первым нециклическим коэффициентом автокорреляции. Если автокорреляция отсутствует, он равен 0. Если же наблюдается полная автокорреляция, то он равен +1 или -1. Отсюда следует, что при отсутствии автокорреляции  , а при полной автокорреляции
, а при полной автокорреляции  =0 или
=0 или  =4.
=4. и нижние
и нижние  приведены в таблице 9.
приведены в таблице 9. ;
; .
. или
или  , то нет статистических оснований ни принять, ни отвергнуть эту гипотезу.
, то нет статистических оснований ни принять, ни отвергнуть эту гипотезу.

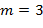



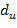
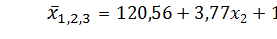 . (46)
. (46)
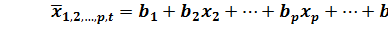 ; (47)
; (47) . (48)
. (48) (переменная
(переменная  . Если он положителен, то с увеличением аргумента происходит рост функции, если отрицателен, – то уменьшение функции. Полученный знак коэффициентов
. Если он положителен, то с увеличением аргумента происходит рост функции, если отрицателен, – то уменьшение функции. Полученный знак коэффициентов  ; (49)
; (49) – среднее значение стандартизованной переменной
– среднее значение стандартизованной переменной  ;
; – значение i -го фактора в стандартизованном масштабе,
– значение i -го фактора в стандартизованном масштабе, . (50)
. (50) = 0,312;
= 0,312;  = 2, 3,…, р) и
= 2, 3,…, р) и 


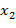

 , (51)
, (51) или
или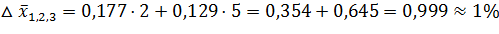
 ) производится корректировка
) производится корректировка  . (52)
. (52) , (53)
, (53) – табличное значение распределения Стьюдента при
– табличное значение распределения Стьюдента при  = 18,755 и,значит, доверительный интервал функции:
= 18,755 и,значит, доверительный интервал функции: .
.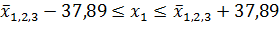
 . (53)
. (53)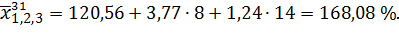

 .
.