
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Проверка исходных данных на нормальность распределения
Корреляционный анализ включает совокупность методов, которые можно разделить на две большие группы. Первая груша – параметрические или собственно корреляционные методы намерения тесноты связи, которые основаны на вычислении различных коэффициентов корреляций. Их применение требует соблюдения двух условий (об одном мы уже говорили): 1) отдельные наблюдения должны быть независимы и 2) эти наблюдения должны быть распределены по нормальному или близкому к нему закону распределения. Вторая группа методов – непараметрические, применение которых не требует соблюдения каких-либо условий и оправдывается в тех частных случаях, когда использование параметрических методов является либо недостаточным (например, при оценке тесноты связи между качественными признаками, обобщении экспертных оценок и т.п.), либо невозможным в силу отсутствия указанных выше условий использования собственно корреляционных методов [18, с. 101 - 107] . Поэтому необходимым и, по сути дела, заключительным этапом предварительной обработки исходных данных является проверка их на нормальность распределения. Простейшим каноническим уравнением кривой нормального распределения Лапласа – Гаусса, график которой представлен на рисунке 5, является следующее:
где
 
Рисунок 5 – Кривая нормального распределения
Кривая симметрична относительно некоторой оси – наибольшей ее ординаты, восстановленной из той точки на оси абсцисс, которая соответствует средней арифметической. Ветви ее асимптотически приближаются к оси абсцисс. Кривая имеет точки перегиба при Центр группировки частот и форма нормальной кривой определяются На симметричном графике В ряду распределения процентов выполнения норм выработки станочников механического цеха – функции рассматриваемой экономико-математической модели – Существует ряд критериев согласия, по которым можно оценить близость распределения в выборках по каждому из факторов исследуемой модели к нормальному распределению. Одним из них является критерий согласия Пирсона или критерий
где Распределение анализируемой выборки является нормальным, если удовлетворяет критерию Романовского:
где К - количество интервалов в анализируемом ряду распределения. Теоретические частоты рада (ординаты кривой нормального распределения) определяются по трансформированной формуле (15):
или
Величина Расчет
Таблица 5 – Расчет
Следует заметить, что сумма теоретических частот должна с принятой точностью совпадать с суммой фактических частот. В данном примере
Определим
Левая часть критерия Романовского:
Поскольку данное отношение меньше 3, распределение процентов выполнения норм выработки станочников механического цеха можно считать нормальным и применять к нему параметрические методы корреляционного анализа. Выборки данных во множественной корреляции являются многомерными. Поэтому проверяется гипотеза о нормальности частных распределений каждого фактора. Если исходные распределения факторов не подчиняются закону нормального распределения, необходимо попытаться их нормализовать. Одним из способов нормализации является замена исходных величин их логарифмами.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 405. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 или
или  , (15)
, (15) – ордината кривой нормального распределения;
– ордината кривой нормального распределения; – среднее квадратическое отклонение признака;
– среднее квадратическое отклонение признака; – нормированное отклонение,
– нормированное отклонение,  ;
; – основание натурального логарифма.
– основание натурального логарифма.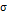 +
+ 

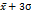 +
+ 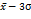 +
+  +
+  +
+  +
+ 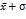 +
+  , т.е. при таких отклонениях значений признака от средней арифметической, которые равны среднеквадратическому отклонению.
, т.е. при таких отклонениях значений признака от средней арифметической, которые равны среднеквадратическому отклонению. = Мо = Ме. При правосторонней асимметрии Мо <
= Мо = Ме. При правосторонней асимметрии Мо <  = 173,72 %; Мо1 = 169 %; Ме1 = 169 %. Имеет место правосторонняя асимметрия. Оценив ее умеренность, т.е. проверим исходные данные этого ряда распределения на нормальность.
= 173,72 %; Мо1 = 169 %; Ме1 = 169 %. Имеет место правосторонняя асимметрия. Оценив ее умеренность, т.е. проверим исходные данные этого ряда распределения на нормальность. (хи-квадрат):
(хи-квадрат): , (16)
, (16) – эмпирическая (фактическая) частота анализируемого ряда распределения в к-й группе;
– эмпирическая (фактическая) частота анализируемого ряда распределения в к-й группе; – его теоретическая частота в к-й группе.
– его теоретическая частота в к-й группе. (17)
(17) – число степеней свободы анализируемого ряда распределения,
– число степеней свободы анализируемого ряда распределения,  ;
;
 (18)
(18) приведена в приложении 6. Она определяется в зависимости от величины t.
приведена в приложении 6. Она определяется в зависимости от величины t. 
 = 173,72;
= 173,72;  = 23,83;
= 23,83;  = 14;
= 14;  =50) приведен в таблице 5.
=50) приведен в таблице 5.





 =
=  .
.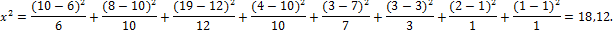
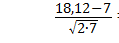 .
.