Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Качественный анализ факторов для отбора в экономико-математическую модельПостроение радов распределения и расчет их характеристик дают возможность провести предварительный качественный анализ связи каждого фактора-аргумента исходной экономико-математической модели с фактором-функцией. В качественном анализе взаимосвязи факторов используют следующие статистические методы: сопоставление параллельных рядов, аналитические группировки, таблицы и поля корреляции. При использовании метода сопоставления параллельных рядов вначале в порядке возрастания или убывания в зависимости от характера исследуемого процесса записываются значения фактора-аргумента. Затем параллельно им располагаются соответствующие значения фактора-функции. Сравнение расположенных таким образом значений дает возможность выявить существование и направленность связи. Используем указанный метод для выявления связи между одним из аргументов рассматриваемой экономико-математической модели – стажем рабочего
Таблица 2 – Сопоставление процентов выполнения норм выработки станочников механического цеха и данных общего стажа их работа
 Просматривая два параллельных ряда (первый ранжирован по Метод аналитических группировок считается в статистике основным для изучения связей медку экономическими факторами. Он позволяет выявить корреляционную зависимость более отчетливо. Процесс установления связи между явлениями начинается с группировки единиц по фактору-аргументу. Затем для фактора-функции по группам, на которые была разбита исходная выборка, вычисляют средние значения. Искусство группировок в корреляционно-регрессионном анализе заключается в том, чтобы образовать такое количество групп (интервалов), при котором в вариации групповых средних в максимальной степени проявилось бы влияние группировочного признака. Для этого следует использовать формулу определения оптимальной величины интервала в построении ряда распределения по фактору-аргументу с учетом следующего правила А.А. Чупрова: "Чем больше групп мы в состоянии нарезать, не наталкиваясь ни на одно исключение, тем прочнее вывод о наличии связи, т.е. оптимальное число групп имеет место в том случае, когда групповые средние перестанут носить случайный характер и в то же время группировочный признак проявит себя в полной мере". Переход от исходного дискретного ряда к интервальному, т.е. процесс группировки, осуществляется на основе расчета оптимальной величины интервала по формуле:
В приведенном примере расчетная оптимальная величина интервала для ряда распределения фактора-аргумента составит
Расчетное значение величины интервала следует округлить до ближайшего числа того же порядка, что и значения исходной выборки. В данном случае это 5 и 6. В соответствии с этими величинами интервалов получаем две возможные группировки с числом групп 8 и 7. Результаты группировок представлены в таблице 3.
Таблица 3 – Группировки данных общего стажа работы станочников механического цеха
Заметим, что при определении границ интервалов необходимо начинать построение ряда, отступая на 0,5 принятой величины интервала влево от наименьшего значения признака, и заканчивать ряд, отступая на 0,5 этой величины вправо от наибольшего значения признака. Так, в первой группировке нижняя граница интервального ряда определится следующим образом: 1 – 0,5·5 = 0. Если какое-либо значение признака совпадает с границей интервала, его следует относить в ту группу, для которой оно является верхней границей. Условие Чупрова выдерживается в обеих группировках, так как величины интервалов не намного отличаются друг от друга. Но с учетом того же правила Чупрова целесообразнее принять первую группировку с большим числом групп. В ней по изменению средних значений фактора-функции Наиболее часто для установления корреляционной зависимости используют корреляционную таблицу. Она систематизирует результаты статистической выборки по двум варьирующим признакам и охватывает два зависимых ряда распределения: один ряд распределения представляет фактор-аргумент, а другой – фактор-функцию. Корреляционная таблица может обеспечить наиболее правильную характеристику связи только в том случае, когда число интервалов по двум признакам примерно одинаковое. Составим корреляционную таблицу для рассматриваемого примера (таблица 4). Число интервалов по
Если взять
Таблица 4 – Корреляционная таблица процентов выполнения норм выработки станочников механического цеха и данных общего стажа их работы
Внутренние клетки таблицы содержат частоты, т.е. показывают число станочников, оказавшихся в соответствующих интервалах по Корреляционная таблица делает возможной оценку интенсивности связи. Интенсивная концентрация частот около диагонали указывает на существование тесной связи между факторами, а рассеивание частот по всей таблице – на отсутствие связи. В рассматриваемом примере связь между факторами На основании корреляционной таблицы строят графическое изображение связи в виде поля корреляции. Поле корреляции строится в прямоугольной системе координат: по оси абсцисс откладывают значения фактора-аргумента, а по оси ординат – значения функции. Указав точками в системе координат значения зависимой и независимой переменных по каждому наблюдению исходной выборки, получают изображение поля корреляции. Поскольку графическое изображение связи в корреляционном поле имеет обычно вид облака точек, графический метод исследования связи иногда называют методом "точечного облака". Заметим, что в каждой внутренней клетке поля проставляется то количество точек, которое соответствует частоте идентичной клетки корреляционной таблицы. Дня рассматриваемого примера поле корреляции показано на рисунке 3.
Рисунок 3 – Поле корреляции процентов выполнения норм выработки станочников механического цеха и данных общего стажа их работы
Поле корреляции дает в основном представление о наличии и направлении связи (прямая или обратная). Поэтому его целесообразно дополнить построением эмпирической линии регрессии, которая позволяет более наглядно спрогнозировать форму связи между исследуемыми факторами. Корреляционная зависимость, как известно, выражается в закономерном смещении рядов распределения фактора-функции при изменении фактора-аргумента. Ранее уже отмечалось, что положение рядов распределения обусловливается значениями различных характеристик и, в частности, значениями средних величин. Поэтому для точной оценки положений рядов распределения функции определяются ее средние значения в каждой груше
Рисунок 4 – Эмпирическая линия регрессии в поле корреляции процентов выполнения норм выработки станочников механического цеха и данных общего стажа их работы
Эмпирическая линия регрессии показывает наличие прямой связи между процентами выполнения норм выработки станочников механического цеха и их общим стажем их работы. Однако связь эта не тесная, так как зигзаги линии регрессии не дают возможности "рассмотреть" прямую или какую-либо кривую, к которой линия регрессии стремится. Такое положение объясняется тем, что на проценты выполнения норм выработки станочников в большей мере, чем стаж их работы, влияют другие факторы, прежде всего объективные: фондовооруженность, энерговооруженность, уровень механизации труда и другие. Эти факторы своим действием затушевывают анализируемую зависимость. Поэтому более точно характер зависимости устанавливают на последующих этапах корреляционно-регрессионного анализа методами математической статистики. Таким же образом строят поля корреляции функции и всех других аргументов, включенных в исходную экономико-математическую модель. В рассматриваемом примере это зависимости процентов выполнения норм выработки станочников Если эмпирическая линия регрессии идет параллельно оси аргумента, т.е. смещения рядов распределения функции по данному аргументу не наблюдается, такой аргумент следует исключить из исходной экономико-математической модели.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 337. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 и функцией – процентом выполнения норм выработки станочников механического цеха
и функцией – процентом выполнения норм выработки станочников механического цеха 
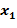
 (14)
(14)


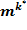


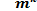 - число наблюдений(частота) в к-й группе;
- число наблюдений(частота) в к-й группе;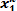 - средняя арифметическая
- средняя арифметическая 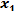 в к-й группе.
в к-й группе. отчетливо прослеживается прямая связь между общим стажем работы станочников механического цеха и процентом выполнения ими норд выработки.
отчетливо прослеживается прямая связь между общим стажем работы станочников механического цеха и процентом выполнения ими норд выработки.
 = 14, то количество интервалов по
= 14, то количество интервалов по 
 и
и 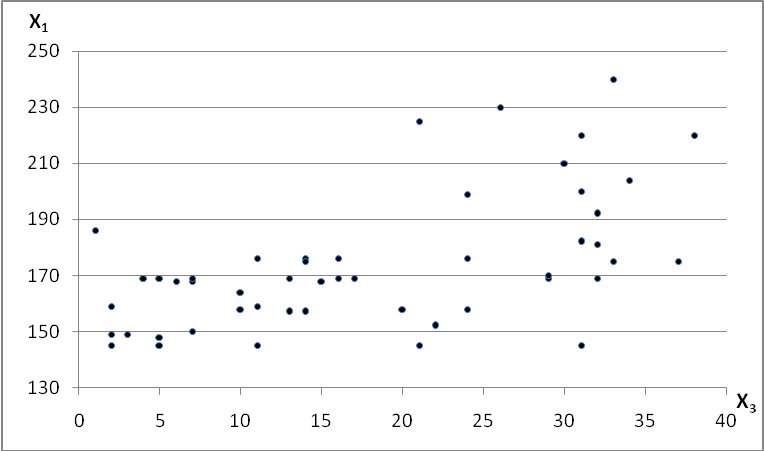
 . Для данного примера значения
. Для данного примера значения