
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Построение рядов распределения, определение их характеристик
Исходным материалом для проведения корреляционно-регрессионного анализа являются ряды распределения, построенные по каждому фактору исходной экономико-математической модели. Ряд распределения - это совокупность значений фактора, записанных в порядке сбора информации (проведения наблюдений). В рассматриваемом примере четыре ряда распределения: первый – по проценту выполнения норм выработки, второй – по возрасту рабочих, третий – по их общему стажу работы, четвертый – по законченному образованию (таблица 1). Если значения анализируемого фактора записать в порядке возрастания их или убывания, получим ранжированный ряд (ранжированный ряд по проценту выполнения норм выработки рабочих записан выше). Аналогично можно построить ранжированные ряды по другим факторам. Характеристики рядов распределения дают возможность проводить количественное описание каждого ряда распределения и их статистическую оценку в процессе корреляционно-регрессионного анализа. Расчет характеристик рядов распределения осуществляется в программах множественной линейной и нелинейной регрессий (приложения 3, 4, 5). В качестве одной из важнейших характеристик рядов распредедения применяют средние величины. Не останавливаясь на их разновидностях, укажем наиболее употребительную – среднюю арифметическую
где
В рассматриваемом ряду распределения процентов выполнения норм выработки рабочих:
В качестве структурной средней характер ряда распределения применяются мода и медиана. Под модой Мо понимают значение фактора, наиболее часто встречающегося в данном ряду. В приведенном примере Mo1=169. Медиана Me – это серединный член ранжированного ряда. При нечетном числе членов ряда ( 
В приведенном примере n = 50, поэтому медиана
В средних величинах выражается количественно типический уровень, который имеют члены исследуемого ряда. Однако по средним величинам нельзя установить характерные черты статистического распределения, которым обладает ряд. Поэтому встает вопрос об оценке вариации (изменения) фактора в его ряду распределения. Самый простой способ оценки вариации состоит в определении разности между наибольшим
Очевидно, что величина такого показателя целиком зависит от случайности расположения крайних членов ряда. Варьирование же значений признака у основной массы членов ряда не находит никакого отражения в этом показателе. Поэтому математическая статистика предпочитает оперировать такими показателями, которые основаны на учете колеблемости значений фактора у всех членов данной совокупности. Эта колеблемость обычно выражается в виде их отклонений от средней арифметической. Наиболее употребительными показателями вариации являются: среднее квадратическое отклонение σ, дисперсия σ2 и коэффициенты вариации. Дисперсия – это средний квадрат отклонений членов ряда от их средней арифметической:
Среднее квадратическое отклонение представляет собой меру колеблемости и вычисляется как средняя квадратическая отклонений членов ряда от их средней арифметической:
Указанные показатели относятся к абсолютным показателям вариации. Кроме них вычисляются и относительные – коэффициенты вариации. Из них наиболее употребительным является коэффициент вариации по среднему квадратическому отклонению
В рассматриваемом примере указанные показатели составляют
Нормальным уровнем колеблемости данных считается интервал 2 – 33 %. Как видим, в рассматриваемом ряду процентов выполнения норм выработки колеблемость данных нормальная, резких перепадов нет. Для основных характеристик рядов распределения можно рассчитать и так называемые стандартные ошибки. Например, стандартная ошибка средней арифметической
Она показывает, как отклоняется средняя арифметическая выборки от значений фактора в генеральной совокупности. Из формулы (10) видно, насколько важное значение при исследованиях имеет большое число наблюдений. При достаточно большом числе наблюдений стандартная ошибка становится настолько малой, что разность между характеристиками выборки и параметрами генеральной совокупности может не приниматься во внимание. Процентное отношение
Этот показатель, как уже отмечалось ранее, заложен в основу таблицы и номограммы достаточно больших чисел и считается допустимым, если не превышает 3 – 5 %. В рассматриваемом примере:
Следовательно, точность проведения исследования по выборке процентов выполнения норм выработки рабочих лежит в допустимых пределах. Стандартная ошибка средней арифметической может быть использована для выяснения однородности изучаемых частичных совокупностей, если выборка составлена из частичных выборок, представленных разными производственными системами. Для этого вычисляется стандартная ошибка
Если
то исследуемые частичные выборки являются разнородными и не могут включаться в общую выборку для проведения по ней корреляционно-регрессионного анализа. В процессе предварительной обработки данных следует проверить все сомнительные члены ряда. Как правило, это крайние члены ранжированного ряда. Прежде всего, необходимо выяснить правильность первичной записи. Если обнаружена грубая ошибка, ее следует исправить. Если же нет возможности проверить первичную документацию, то для ответа на вопрос, является ли значительное отличие "выскакивающего" значения от других результатом случайной вариации или это отличие выходит за ее пределы и данный вариант как ошибочный подлежит исключению из ряда, необходимо сопоставить его с σ ряда. Если "выскакивающий" вариант отличается от средней арифметической более чем на 4σ, то он может быть исключен как не относящийся к данной однородной совокупности. Выявление промахов и исключение сомнительных вариантов нецелесообразно при n < 6. Предположим, что в рассмотренном ранее ряду процентов выполнения норм выработки сомнение вызывает крайний вариант |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 321. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 :
: 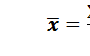 , (4)
, (4) – значение j –го члена ряда.
– значение j –го члена ряда.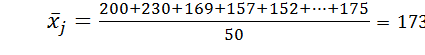 .
.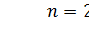 ) медианным будет значение члена ранжированного ряда с номером
) медианным будет значение члена ранжированного ряда с номером  , при четном числе членов ряда медиана определяется по формуле:
, при четном числе членов ряда медиана определяется по формуле: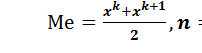 (5)
(5)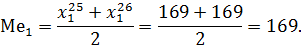
 и наименьшим
и наименьшим 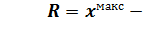 (6)
(6)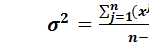 (7)
(7)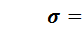 (8)
(8) :
: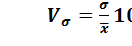 (9)
(9)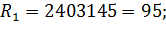
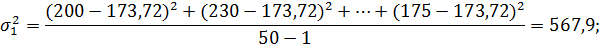
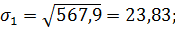
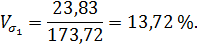
 определяется так:
определяется так: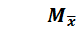 (10)
(10) выражает точность проведения исследования ε:
выражает точность проведения исследования ε: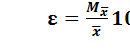 (11)
(11)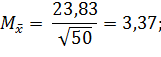
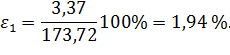
 разности средних значений выборок
разности средних значений выборок  и
и 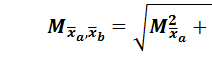 (12)
(12)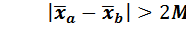 (13)
(13) = 240. Он отличается от средней арифметической ряда
= 240. Он отличается от средней арифметической ряда  = 173,72 на величину 68,28. Сопоставляя эту величину c
= 173,72 на величину 68,28. Сопоставляя эту величину c  всего лишь на 2,78 σ , что значительно меньше 4σ. Следовательно, вариант
всего лишь на 2,78 σ , что значительно меньше 4σ. Следовательно, вариант