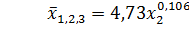Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
СОСТАВЛЕНИЕ И РЕШЕНИЕ УРАВНЕНИЙ РЕГРЕССИИ
Следующим этапом корреляционно-регрессионного анализа является выбор математической формы связи фактора-функции с каждым фактором-аргументом, включенным в экономико-математическую модель, и решение соответствующего уравнения связи, называемого иначе уравнением регрессии. В общем виде уравнение регрессии записывается в виде:
где
Корреляционная зависимость может принимать различную форму. В одних случаях с возрастанием фактора-аргумента функция растет или убывает равномерно, в других это убывание или возрастание происходит неравномерно. Существует большое количество аналитических функций, используемых в корреляционно-регрессионном анализе [24, с. 34 – 45]. Однако наиболее употребительными в экономическом корреляционно-регрессионном анализе являются следующие функции: линейные: степенные: линейно-логарифмические: Значительное распространение указанных зависимостей связано с простотой расчета и удобством использования самих регрессионных уравнений на практике. При связях линейных или близких к ним применяют линейные зависимости, при криволинейных – степенные. На исключено, конечно, использование и более сложных математических функций. Однако практически это делается редко, так как сложные функции не только трудно экономически истолковать, но и трудно рассчитать, даже используя современные ЭВМ. Выбор той или иной формы связи диктуется рядом соображений и является, пожалуй, самым сложным вопросом всего корреляционно-регрессионного анализа, отдаваемым "на откуп" исследователю. Эти соображения сводятся к следующему:  1) выбранная функция должна отражать закономерности, присущие социалистическому народному хозяйству. Так, при изучении темпов роста производительности труда неверным будет использование связи в форме синусоиды; 2) аналитическая функция должна, по возможности, иметь более простой вид и соответственно минимальное число коэффициентов регрессии. Процесс выбора формы связи начинается на этапе предварительной обработки исходной информации в ходе качественного анализа факторов при включении их в экономико-математическую модель. Он проводится на базе теории той конкретной экономической науки, которая занимается изучением моделируемого процесса, с учетом опыта предыдущих аналогичных исследований. Кроме того, ориентировочное представление о форме связи функции с каждым аргументом можно получить, анализируя соответствующее поле корреляции и эмпирическую линию регрессии. Этот путь основан на действии закона больших чисел, поэтому может дать удовлетворительный результат только при значительном числе наблюдений. Мысленно устраняя те зигзаги графика, которые можно предположить случайными, получаем представление о типе кривой, лежащей в его основе. При малом числе наблюдений такой путь невозможен. Вообще риск субъективного и произвольного выбора здесь очень велик. Разные исследователи на основе одного и того же графика могут прийти к разным выводам относительно формы связи. Относительно рассматриваемой зависимости процентов выполнения норм выработки станочников от общего стажа их работы (см. рисунок 4) связь с одинаковой вероятностью можно предположить и прямолинейной, и криволинейной формы. Следует отметить, что наиболее часто при выборе формы связи двух переменных приходится решать, является связь линейной или нет. Ответить на этот вопрос можно, сравнивая вычисленные коэффициент парной корреляции
то предположение о прямолинейной форме связи оправдано. Если
оценивают существенность различий Один из способов такой оценки заключается в следующем. Определяют величину
где Если обозначить
Величина
Таким образам, предположение о нелинейности связи Выбор формы связи осуществляется попарно для функции и каждого аргумента, т.е. вначале происходит установление линейности одномерных зависимостей Решение указанных уравнений осуществляется программами линейной REGRLIN и нелинейной REGRNEL регрессий, обращение к которым приведено в приложениях 9, 10. Решение уравнения регрессии заключается в поиске коэффициентов Указанные программы REGRLIN и REGRNEL моделируют уравнения регрессии по принципу шаговой регрессии, т.е. постепенно, по шагам включая факторы-аргументы в уравнение. Это включение происходит по мере убывания абсолютной величины парных коэффициентов корреляции, характеризующих связь функции с соответствующими аргументами. В рассматриваемом примере первым включается в уравнение регрессии
в случае нелинейной связи (см.приложение 5):
На втором шаге в уравнение регрессии включается переменная линейное: степенное: Необходимо выбрать из этих уравнений одно, более адекватно описывающее моделируемый процесс зависимости процентов выполнения норм выработки станочников от их законченного образования и общего стажа работы. Его можно будет использовать либо для анализа резервов роста производительности труда в сфере субъективных факторов, либо для планирования индивидуальных заданий рабочим по росту производительности труда, либо для разработки планов социального развития коллективов, задаваясь исходными значениями параметров Поэтому следующим этапом корреляционно-регрессионного анализа является экономико-статистический анализ уравнений регрессии, в ходе которого осуществляется проверка адекватности полученных уравнений регрессии моделируемому процессу.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 312. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
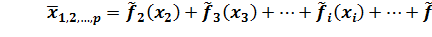 , (29)
, (29) – расчетное значение функции
– расчетное значение функции  , соответствующее заданным значениям аргументов
, соответствующее заданным значениям аргументов  ;
; – одномерная зависимость
– одномерная зависимость  .
. ; (30)
; (30) ; (31)
; (31) , (31а) где
, (31а) где  – искомые коэффициенты регрессии для выбранной формы связи (
– искомые коэффициенты регрессии для выбранной формы связи (  =2,3,…,p), показывающие к какому изменению функции приводит изменение на единицу i -го аргумента.
=2,3,…,p), показывающие к какому изменению функции приводит изменение на единицу i -го аргумента. и корреляционное отношение
и корреляционное отношение  . Если
. Если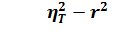 , (32)
, (32) ,
, , (33)
, (33) – ошибка разности между
– ошибка разности между 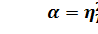 , то
, то . (34)
. (34) < 2 свидетельствует о несущественности различия и, значит, о линейности связи, В рассматриваемом примере
< 2 свидетельствует о несущественности различия и, значит, о линейности связи, В рассматриваемом примере  = 0,57,
= 0,57,  = 0,59, т.е.
= 0,59, т.е. 
 связь между
связь между  = 0,28, a
= 0,28, a 
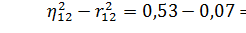 .
. определяется ее вид. Это будет функция либо вида (30), либо вида (31). Целесообразно составить и решить оба уравнения, а затем выбрать наиболее адекватное исследуемому процессу по результатам решения: F-критерию. Т-критерию, остаточной сумме квадратов, средней ошибке аппроксимации. Именно такой подход применим к рассматриваемому примеру, так как у одного из двух аргументов, включенных в экономико-математическую модель, связь с функцией линейна, а у другого – нелинейна.
определяется ее вид. Это будет функция либо вида (30), либо вида (31). Целесообразно составить и решить оба уравнения, а затем выбрать наиболее адекватное исследуемому процессу по результатам решения: F-критерию. Т-критерию, остаточной сумме квадратов, средней ошибке аппроксимации. Именно такой подход применим к рассматриваемому примеру, так как у одного из двух аргументов, включенных в экономико-математическую модель, связь с функцией линейна, а у другого – нелинейна. для выбранного уравнения регрессии на основе исходных выборок функции
для выбранного уравнения регрессии на основе исходных выборок функции  и фактических
и фактических  ;
; .
.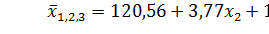 ;
;