
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обеспечение необходимого объема и случайного состава выборкиВ соответствии с исходной экономико-математической моделью исследуемого процесса осуществляют сбор исходной информации и ее предварительную обработку. От тщательности выполнения этого этапа моделирования во многом зависит качество искомого уравнения регрессии. К исходным данным предъявляют следующие требования: 1) исходные данные должны быть достоверными, так как в противном случае они приведут к ложным корреляционно-регрессионным выводам, опасны искажения, вызванные изменениями цен, изменениями в ассортименте выпускаемой продукции, организационными перестуками и т.д.; 2) исходные данные должны быть однородными. Критикуя земских статистиков за то, что в их работе сравнивались разнородные типы крестьянских хозяйств, В.И.Ленин писал: "и… главной причиной путаницы было то, что сравнивались хозяйства неоднородные, поставленные в различные общественные условия, отличающиеся по самому типу ведения хозяйства" [1, с. 25]; 3) совокупность исходных данных должна быть случайной и достаточной по количеству. Наиболее полно последнее требование может быть реализовано в том случае, если анализу подвергнуть все единицы общей (генеральной) совокупности. В рассматриваемом примере это должна быть вся совокупность станочников механического цеха обследуемого завода. Однако такой анализ практически осуществить невозможно, так как для этого потребуется много времени и труда. Поэтому прибегают к ограниченному числу наблюдений, которое получило название выборки. Для правомерности выборки необходимо, чтобы характеристики ее были достаточно близки по своим значениям к характеристикам генеральной совокупности. Поэтому перед сбором исходных данных решают два вопроса:  1) какое число единиц должно входить в выборку, чтобы по ней можно было делать надежные выводы об изучаемом процессе; 2) из каких именно единиц генеральной совокупности надо составить выборку, чтобы ее можно было рассматривать в качестве представительного образца изучаемой генеральной совокупности. В математической статистике ответ на первый вопрос дают таблица достаточно больших чисел и номограмма достаточно больших чисел. Таблица достаточно больших чисел (приложение 1) составлена на основании формулы, которая показывает, как достаточно большое число наблюдений (объем выборочной совокупности η) зависит от "степени уверенности" и величины допустимой ошибки ε. "Степень уверенности" определяется величиной вероятности р, с которой делается соответствующее заключение. Относительно выбора величины р нет какого-либо .решения, одинакового для всех исследований. Чем ближе к единице будет величина рассматриваемой вероятности, тем надежнее будет заключение, В практике научных исследований обычно принимается р = 0,95 или Р = 0,99. Допустимая ошибка ε устанавливается обычно равной 0,03 – 0,05 (или 3-5 %). Чтобы по таблице достаточно больших чисел найти число наблюдений, надо задать р и ε. Например, при р = 0,95 и ε = 5 % объем выборки составит 384 наблюдения. Если же по проводившимся ранее исследованиям известна мера изменчивости показателя V[2], то объем выборки приятой же самой величине вероятности р и допустимой ошибке εможет быть найден при помощи номограммы достаточно больших чисел (приложение 2), Она построена для р=0,95, обычно принимаемой в практике научных исследований. Если V ≤ 10 %, то объем выборки находится по номограмме непосредственно. Зная V и задаваясь ε, проводим мысленную прямую через соответствующие точки двух крайних шкал, тогда точка пересечения мысленной прямой с серединной шкалой даст искомое количество наблюдений. Если V > 10%, то полученное на серединной шкале число нужно умножить на 100, Например, при р = 0,95, ε = 0,05, V = 16 объем выборки составит 39 наблюдений (0,39 * 100). Нетрудно заметить, что номограмма достаточно больших чисел дает числа значительно меньшие, чем таблица достаточно больших чисел. Это объясняется тем, что номограмма предусматривает небольшую изменчивость признака – менее 50 % [23, с, 22] . Зная, что в проводимом исследовании имеет место малая изменчивость наблюдаемого признака, можно и нужно пользоваться номограммой достаточно больших чисел. Существуют и другие рекомендации к обоснованию необходимого объема выборки [10, с. 189-192]. В том случае, когда нет возможности собрать указанную представительную выборку, следует исходить из имеющегося объема выборки, установив по таблице достаточно больших чисел величину вероятности р и допустимую ошибку ε, которые будут характеризовать надежность последующих выводов. После определения необходимого объема выборки остается решить второй вопрос: какие именно единицы генеральной совокупности должны войти в выборку. Чтобы выборка правильно отражала свойства общей совокупности, необходимо каждую единицу брать наугад, т.е. случайно. Для этого применяют следующий способ: 1) составляют список всех единиц генеральной совокупности и нумеруют; 2) из таблицы случайных чисел во второй список выписывают, начиная с какого-либо столбца таблицы, какое количество чисел, которое равно количеству наблюдений в выборке [23, с. 492]; 3) из составленного первого списка берется число наблюдений, равное объему выборки, соответственно полученным номерам второго описка. Однако очень часто нет возможности провести выборку указанным способом, поэтому результаты наблюдений, т.е. элементы имеющейся выборки, проверяют на случайность и независимость результатов наблюдений. Такая проверка связана с тем, что применение наиболее употребительных статистических методов корреляционно-регрессионного анализа основано на результатах ряда независимых испытаний, образующих случайную выборку. Случайность выборки интерпретируется как обеспечение равновероятности попадания каждого наблюдения из генеральной совокупности в выборку. Одним из методов проверки имеющейся выборки на случайность является метод серий, основанный на медиане выборки. Пусть имеется выборка
Если хотя бы одно из этих неравенств окажется нарушенным, гипотезу о случайности выборки следует отбросить. Следует заметить, что в корреляционно-регрессионном анализе участвует не одномерная, а многомерная выборка (в случае парной корреляции – это двумерная выборка). Проверять на случайность выборку по каждой переменной нецелесообразно. Достаточно ограничиться проверкой показателя-функции Приведенные, а также все последующие положения теории корреляционно-регрессионного анализа будем рассматривать по следующей исходной экономико-математической модели:
где
Исходные данные были собраны в одном из механических цехов Тульского комбайнового завода (таблица 1). Таблица 1 – Исходная выборка
Проверим на случайность выборку показателя 200+ 230+ 169 157– 152– 168– 199+ 157– 169 168– 175+ 204+ 148– 169 145– 240+ 169 170+ 158– 210+ 175+ 169 169 169 158– 181+ 168– 182+ 158– 145– 175+ 150– 164– 220+ 145– 159– 176+ 159– 145– 220+ 145– 149– 225+ 176+ 169 176+ 192+ 149– 186+ 175+ Строим ранжированный ряд в порядке возрастания 145, 145, 145, 145, 145, 148,149,149, 150, 152, 157, 157,158, 158, 158, 59, 159, 164,168,168, 168, 169, 169, 169,169, 169, 163, 169, 169, 170,175,175, 175, 175, 176, 176,176, 181, 182, 186, 192, 199, 200, 204, 210, 220, 220, 225, 230, 240. Медиана равна 169,
Следовательно, выборка случайна, на ее основе можно проводить корреляционно-регрессионный анализ. Заканчивая основные рекомендации по cбору исходной информации, добавим, что методические вопросы правильного сбора информации, связанные с обеспечением минимального количества ошибок при ее сборе, подробно описаны в ряде работ [10, с.179-189; 15, с. 26-27; 13, гл.13; 18, с. 7-13]. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 311. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 из некоторой генеральной совокупности. Составим из нее ранжированный ряд
из некоторой генеральной совокупности. Составим из нее ранжированный ряд  Определил медиану полученного ряда Me. Затем возвращаемся к исходной выборке
Определил медиану полученного ряда Me. Затем возвращаемся к исходной выборке  и будем вместо каждого значения
и будем вместо каждого значения  ставить плюс, если
ставить плюс, если  и протяженностью самой длинной серии
и протяженностью самой длинной серии  ,где под серией понимается последовательность подряд идущих плюсов или подряд идущих минусов (в частном случае серия может состоять только из одного плюса или одного минуса и ее протяженность тогда будет равна единица). Очевидно, что если выборка случайна, то чередование плюсов и минусов в такой последовательности должно быть более или менее случайным, т.е. эта последовательность не содержит слишком длинных серий. Соответственно общее число серий
,где под серией понимается последовательность подряд идущих плюсов или подряд идущих минусов (в частном случае серия может состоять только из одного плюса или одного минуса и ее протяженность тогда будет равна единица). Очевидно, что если выборка случайна, то чередование плюсов и минусов в такой последовательности должно быть более или менее случайным, т.е. эта последовательность не содержит слишком длинных серий. Соответственно общее число серий  (2)
(2) .
. , (3)
, (3)
 = 4. Тогда условия (2) запишутся так:
= 4. Тогда условия (2) запишутся так: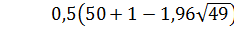 , т.е. 25 > 18;
, т.е. 25 > 18; , т.е. 4<6,64.
, т.е. 4<6,64.