
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ИЗМЕРЕНИЕ СТЕПЕНИ ТЕСНОТЫ СВЯЗИ MEЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ
После предварительной обработки исходной информации становится возможной количественная оценка интенсивности связи между исследуемыми переменными. Она производится с помощью коэффициентов корреляции (парных и множественных) – в случае линейной связи и корреляционных отношений – в случае нелинейной связи. Парный коэффициент корреляции
Коэффициент корреляции является отвлеченным числом и не зависит от единиц, в которых измерялись значения В советской литературе принято оценивать степень тесноты связи между исследуемыми переменными по следующей шкале: - если - если 0,З - если Помимо отмеченных коэффициент корреляции обладает еще следующими свойствами: - при - при В случае множественной корреляции расчет парных коэффициентов корреляций между парой исследуемых переменных приводит к образованию матрицы парных коэффициентов. Для рассматриваемой экономико-математической модели влияния субъективных факторов производительности труда на процент выполнения норм выработки станочников механического цеха матрица парных коэффициентов корреляции приведена в приложении 3. Наиболее сильной оказалась связь между функцией и общим стажем работа станочников (  Полученные при этом парные коэффициенты корреляции имеют вполне определенное толкование. Так, например, коэффициент корреляции При анализе парных коэффициентов корреляции необходимо обратить внимание на наличие в экономико-математической модели мультиколлинеарности, под которой понимается наличие функциональной или близкой к ней связи между факторами (показателями). В качестве своеобразных индикаторов возможного наличия мультиколлинеарности выступают парные коэффициенты корреляции факторов-аргументов .Если коэффициент корреляции больше 0,8, это говорит о наличии в модели мультиколлинеарности. Мультиколлинеарность снижает надежность оценок параметров экономико-математической модели, приводит к неверным выводам, поэтому при ее обнаружении мультиколлинеарные факторы подлежат исключению из модели. В рассматриваемом примере коллинеарны два фактора: возраст рабочих Таким образом, на этапе определения тесноты связи между исследуемыми переменными происходит дальнейшее уточнение исходной экономико-математической модели. Для рассматриваемого примера она формулируется теперь следующим образом: по данным табеля, имеющейся отчетности, опроса, найти аналитическое выражение, показывавшее, как связаны между собой процент выполнения норм выработки станочников механического цеха Тульского комбайнового завода
Линейный коэффициент корреляции достаточно точно оценивает степень тесноты связи в случае линейной зависимости между признаками. При наличии же нелинейной зависимости он недооценивает степень тесноты связи. Поэтому при необходимости точной оценки степени тесноты связи в случае криволинейной корреляции между признаками
где
Заметим, что в отличие от линейных коэффициентов корреляции Рассчитаем
Таблица 6 – Расчет
Поэтому практически и в случае нелинейной корреляции основным показателем оценки тесноты связи между двумя переменными остается парный коэффициент корреляции, хотя он несколько снижает результат. Это нашло отражение и в рекомендуемой машинной программе расчета параметров нелинейной регрессии (см. приложение 5).
Значение Аналогичным образом было рассчитано отношение На практике корреляционное отношение как показатель оценки тесноты связи широкого применения не получило, так как, во-первых, оно не оценивает направления связи (ибо изменяется только от 0 до +1), и, во-вторых, требует построения группировочных таблиц большого числа наблюдений. Помимо парных коэффициентов корреляции рассчитывают еще и частные коэффициенты корреляции. Они позволяют выявить "чистую" зависимость факторов друг от друга при условии, что значения остальных факторов остаются постоянными. Поэтому абсолютные значения частных коэффициентов корреляции не могут быть больше коэффициента множественной корреляции. В рассматриваемой модели (20) имеем следующие частные коэффициента корреляции (см. приложение 4): Тесноту связи между функцией и совокупностью всех аргументов в случае множественной корреляции характеризует множественный коэффициент корреляции
где В программах множественной линейной и нелинейной регрессий При малом числе наблюдений значение
где В рассматриваемом примере линейной регрессии (см. приложение 4) на втором шаге регрессии множественный коэффициент корреляции уменьшен с Вариация функции складывается под влиянием факторов как введенных в модель, так и не учтенных в модели. Квадрат коэффициента корреляции После расчета коэффициентов корреляции необходимо проверить их существенность, т.е. в какой мере полученные значения коэффициентов корреляции в выборочных совокупностях распространяются на соответствующие генеральные совокупности. В качестве критерия значимости (надежности) парных и частных коэффициентов корреляции может быть применено значение распределения Стьюдента
В программах регрессий
то коэффициент корреляции в генеральной совокупности заметно отличен от 0, т.е. данный коэффициент корреляции существен. Для оценки надежности множественного коэффициента корреляции (детерминации) используется критерий Фишера:
с
то связь существенна. Значения
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 320. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 характеризует связь между двумя случайными величинами
характеризует связь между двумя случайными величинами  и
и  при условии линейной корреляции между ними. Он рассчитывается по формуле:
при условии линейной корреляции между ними. Он рассчитывается по формуле: (19)
(19) изменяется в среднем случайная величина
изменяется в среднем случайная величина  лежит в пределах от -1 до +1. Чем выше значение
лежит в пределах от -1 до +1. Чем выше значение  , тем теснее связь между переменными и тем с большим основанием найденная впоследствии связь между переменными может быть использована в анализе, прогнозировании и т.п.
, тем теснее связь между переменными и тем с большим основанием найденная впоследствии связь между переменными может быть использована в анализе, прогнозировании и т.п. 0,3, – связь слабая;
0,3, – связь слабая; 0,7 – связь средняя;
0,7 – связь средняя; наблюдается не корреляционная, а функциональная связь;
наблюдается не корреляционная, а функциональная связь; – связь прямая, при
– связь прямая, при  = 0,28 показывает, что при повышении станочником уровня своего образования на
= 0,28 показывает, что при повышении станочником уровня своего образования на  .
. . (20)
. (20) , (21)
, (21) – дисперсия признака
– дисперсия признака  – межгрупповая дисперсия признака
– межгрупповая дисперсия признака  . (22)
. (22)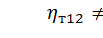 .
. для оценки тесноты связи между процентом выполнения норм выработки станочников механического цеха и их общим стажем работы (см. таблицу 3). Анализ поля корреляции и формы эмпирической линии регрессии не исключает криволинейной связи между функцией и указанным аргументом (см. рисунок 4). Сведем расчет
для оценки тесноты связи между процентом выполнения норм выработки станочников механического цеха и их общим стажем работы (см. таблицу 3). Анализ поля корреляции и формы эмпирической линии регрессии не исключает криволинейной связи между функцией и указанным аргументом (см. рисунок 4). Сведем расчет  в таблицу 6 (
в таблицу 6 ( 

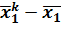


 .
. = 0,38;
= 0,38;  = -0,27, Они по абсолютной величина выше соответствующих парных коэффициентов корреляции (
= -0,27, Они по абсолютной величина выше соответствующих парных коэффициентов корреляции (  . Он положителен, изменяется от 0 до +1 и определяется по формуле:
. Он положителен, изменяется от 0 до +1 и определяется по формуле: , (23)
, (23) – коэффициент регрессии при i-й переменной в стандартизованном масштабе.
– коэффициент регрессии при i-й переменной в стандартизованном масштабе. увеличивается от 0,566 до 0,647 по мере включения в уравнение обоих факторов-аргументов (см, приложение 4).
увеличивается от 0,566 до 0,647 по мере включения в уравнение обоих факторов-аргументов (см, приложение 4). , (24)
, (24) – множественный коэффициент корреляции, скорректированный с учетом степеней свободы.
– множественный коэффициент корреляции, скорректированный с учетом степеней свободы. = 0,637. Именно последнее значение и показывает истинную степень тесноты связи между процентом выполнения норм выработки станочников и введенным в модель субъективными факторами. По приведенной выше шкале указанная связь может быть отнесена к связям средней интенсивности. Сравнивая при этом коэффициенты множественной корреляции, вычисленные по программам линейной и нелинейной регрессий (см. приложения 4,5), видим, что в случае нелинейной регрессии коэффициент множественной корреляции ниже, т.е.
= 0,637. Именно последнее значение и показывает истинную степень тесноты связи между процентом выполнения норм выработки станочников и введенным в модель субъективными факторами. По приведенной выше шкале указанная связь может быть отнесена к связям средней интенсивности. Сравнивая при этом коэффициенты множественной корреляции, вычисленные по программам линейной и нелинейной регрессий (см. приложения 4,5), видим, что в случае нелинейной регрессии коэффициент множественной корреляции ниже, т.е.  <
<  (0,556<0,637). Объясняется это использованием при расчете
(0,556<0,637). Объясняется это использованием при расчете  = 0,418) представляет квадрат множественного коэффициента корреляции функции и совокупности двух факторов-аргументов. В данном случае величина
= 0,418) представляет квадрат множественного коэффициента корреляции функции и совокупности двух факторов-аргументов. В данном случае величина  :
: . (25)
. (25) степеней свободы и задаваемого уровня значимости. Наиболее распространенным является уровень 0,05. Если
степеней свободы и задаваемого уровня значимости. Наиболее распространенным является уровень 0,05. Если . (26)
. (26) . (27)
. (27) и
и  степенями свободы. В программах множественной регрессии значения
степенями свободы. В программах множественной регрессии значения  распечатаны после вектора коэффициентов множественной детерминации. Если
распечатаны после вектора коэффициентов множественной детерминации. Если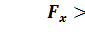 , (28)
, (28) приведены в приложении 8 для уровня значимости 0,05. В рассматриваемом примере при
приведены в приложении 8 для уровня значимости 0,05. В рассматриваемом примере при