
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Однорідна система рівнянь. Фундаментальна система розв'язків однорідної системи рівнянь.Розглянемо однорідну систему лінійних алгебраїчних рівнянь
Використовуючи знак підсумовування, і-те рівняння системи (1) можна записати в вигляді
А тоді всю систему (1) можна подати в вигляді Для системи (1) розв’яжемо задачі, які ставляться в теорії лінійних алгебраїчних рівнянь: 1) питання сумісності; 2) питання визначеності і невизначеності. Зрозуміло, що будь-яка однорідна система має розв’язок (0,0,…,0) (його називають нульовим або тривіальним), тому однорідна система завжди сумісна. Цей же результат випливає з теореми Кронекера-Капеллі, яка виконується для будь-якої однорідної системи. З’ясуємо умови визначеності однорідної системи, застосувавши вже відомий критерій: · Якщо ранг rA=n (n- кількісь невідомих), то система (1) має лишеодин розв’язок – нульовий, і система (1) є визначеною. · Якщо ранг rA<n (n- кількісь невідомих), то система (1) має безліч розв’язків і система (1) є невизначеною. Розглянемо властивості розв’язків однорідної системи. Властивість 1. Сума двох розв’язків однорідної системи є також розв’язком цієї системи. Властивість 2. Добуток розв’язку однорідної системи на деяке число є також розв’язоком однорідної системи. Доведення. Доведемо першу властивість, а друга доводиться аналогічно. Нехай Розглянемо систему в вигляді (1’). Тоді з означення розв’язку, маємо системи правильних числових рівностей: 


Підставимо в ліву частину системи (1’) – замість
Отже З доведених властивостей випливає. Наслідок. Будь-яка лінійна комбінація будь-яких розв’язків однорідної системи є також розв’язком цієї системи. Введемо важливе для однорідної системи поняття фундаментальної системи розв’язків. Означення.Максимальна лінійно незалежна система розв’язків однорідної системи рівнянь називається її фундаментальною системою. З цього означення випливає, що фундаментальна система розв’язків задовольняє дві умови: 1) розв’язки, що входять до фундаментальної системи – лінійно незалежні; 2) будь-який інший розв’язок є лінійною комбінацією цих розв’язків. З’ясуємо скільки розв’язків входить до фундаментальної системи. Розв’язок системи лінійних алгебраїчних рівнянь можна розглядати як вектор n-вимірного арифметичного простору. Раніше було доведено, що в n-вимірному арифметичному просторі найбільша кількість лінійно-незалежних векторів містить n-векторів. Отже маємо попередній висновок: фундаментальна система розв’язків містить не більше n розв’язків. Більш точну інформацію містить наступна теорема. Теорема. (про фундаментальну систему розв’язків) Якщо ранг p матриці A менше кількості невідомих n, то однорідна система рівнянь має фундаментальну систему розв’язків, причому кількість розв’язків, що входить до фундаментальної системи дорівнює n-p. Доведення. Нехай задано однорідну систему рівнянь
Нехай ранг матриці
Тоді кількість фундаментальних розв’язків (n-p). З того , що ранг rA=p<n випливає , що система (1) невизначена, тобто має безліч розв’язків. Запишимо всі розв’язки в вигляді (**) (зробивши попередньо для системи (1) припущення, при яких було отримано (**)). Виберемо з цієї нескінченної множини розв’язків, (n-р) розв’язков за таким правилом : 1. Надамо вільним невідомим значення Підставимо ці значення в формулу (**) , отримаємо значення для
2. Надамо вільним невідомим другий раз інші значення …. Надамо вільним невідомим (n-p) раз значення Підставимо їх в (**), отримаємо
Отже ми отримали систему розв’язків: 1-ий розв’язок ( 2-ий розв’язок ( … ( Зауважимо, що вільні невідомі в розв’язках (2) вибирались будь-як, але за однією умовою Доведемо, що система розв’язків (2) є фундаментальною. Для цього ми повинні довести, що : 1. Розв’язки (2) лінійно незалежні. 2. Приєднання до (2) будь-якого розв’язку системи приводить до лінійно залежної системи. Для доведення першого пункту розглянемо матрицю К :
1. Доведемо rK=n-p. Це випливає з того що в цій матриці за умовою (3) є мінор порядку (n – p), що не дорівнює нулю. Мінорів більш високого порядку не можна скласти. Тоді з теореми про ранг матриці rK = n – p. З того, що rK = n – p , використовуючи другий наслідок з теореми про ранг випливає, що в матриці К є лише (n – p) лінійно незалежних рядків. А в рядках записано розв’язки (2), тобто вони лінійно незалежні. 2. Для доведення другого пункту розглянемо довільний розв’язок системи (1)
Доведемо, що ранг і цієї матриці дорівнює r Доведемо, що в цій матриці лише (n – p) лінійно незалежних стовпців. Саме з цього тоді випливатиме, що r Доведемо, що перший, другий, і т.д. р-ий стовпчик матриці Насправді, в першому стовпчику матриці Тобто в матриці Теорему доведено. Зауваження. Якщо rА = р = n , то в цьому випадку система визначена, має один тривіальний розв’язок, а система з одного нульововго вектора лінійно залежна, тому фундаментальної системи розв’язків немає. Розглянемо множину розв’язків однородної системи з точки зору векторного простору. Множина розв’язків однорідної системи є підмножиною n-вимірного арифметичного простру. Більш того з властивостей розв’язків однорідної системи випливає, що в цій підмножині визначені операції додавання векторів і множення вектора на число. Тоді як випливає з попереднього множина усіх розв’язків однорідної системи є підпростором арифметичного простору. Базисом цього підпростору є фундаментальна система розв’язків. З тереми про фундаментальну систему випливає, що вимірність цього підпростору дорівнює n-r (n – кількість невідомих, r – ранг матриці системи). |
||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 347. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1)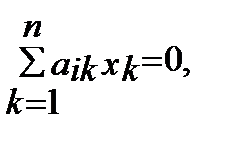

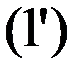
 і
і  – розв’язки системи (1). Треба визначити, чи є
– розв’язки системи (1). Треба визначити, чи є 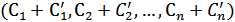 розв’язком системи (1).
розв’язком системи (1). .
.
 (1)
(1) = p.
= p. ,
,  (**)
(**)

 .
.
 . Підставимо в (**), отримаємо другий розв’язок.
. Підставимо в (**), отримаємо другий розв’язок.
 .
.
 )
) ) (2)
) (2)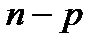 ) розв’язок (
) розв’язок (  )
) (3)
(3)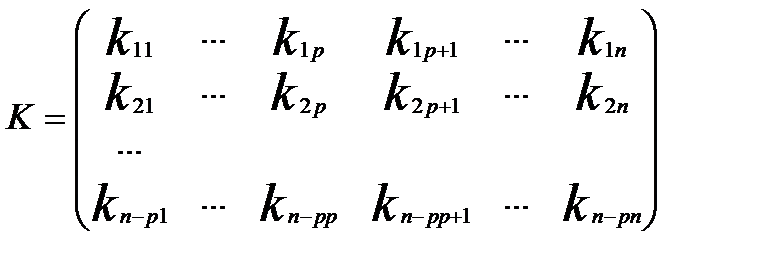
 . Приєднаємо його до системи розв’язків (2) і доведемо, що отримана система розв’язків вже лінійно залежна. Для цього утворимо матрицю
. Приєднаємо його до системи розв’язків (2) і доведемо, що отримана система розв’язків вже лінійно залежна. Для цього утворимо матрицю 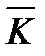 :
: .
. = n – p.
= n – p. = n – p. З того, що мінор в правому верхньому куту не дорівнює нулю, випливає, що останнні ( n – p ) стовпців матриці лінійно незалежні. Доведення цього факту таке ж саме як і в першій частині про ранг.
= n – p. З того, що мінор в правому верхньому куту не дорівнює нулю, випливає, що останнні ( n – p ) стовпців матриці лінійно незалежні. Доведення цього факту таке ж саме як і в першій частині про ранг. є лінійною комбінацією останніх ( n – p ) стовпців. Це твердження випливає з формули (**).
є лінійною комбінацією останніх ( n – p ) стовпців. Це твердження випливає з формули (**).