Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Застосування теорії визначників до лінійних систем алгебраїчних рівнянь. Теорема Крамера та лема до неїЛема. Нехай задано визначник d n-го порядку. Сума добутків елементів і-го рядка на алгебраїчні доповнення до відповідних елементів j-го рядка дорівнює 0. Доведення. Нехай задано довільний визначник:
Доведемо, що Для доведення побудуємо допоміжний визначник, який буде відрізнятися від визначника d лише одним рядком.
Цей визначник за властивістю 4 дорівнює 0. Застосуємо до j-го рядка визначника наслідок з теореми Лапласа.
Залишилось довести, що Означення. Визначником системи називається визначник складений з коефіцієнтів при невідомих. Теорема Крамера. Нехай задано систему n алгебраїчних рівнянь з n невідомими, визначник якої не нульовий. Тоді невідома xk дорівнює дробу, знаменником якого є визначник системи, а чисельником також є визначник, який можна отримати з визначника системи заміною k-го стовпця стовпцем вільних членів. Доведення. Розглянемо систему
Помножимо обидві частини 1-го рівняння на А1k, 2-го на А2k, n-го на Аnk. Тоді отримаємо
Введемо в розгляд деякий визначник.
Застосуємо до k-го рядка цього визначника наслідок теореми Лапласа Застосуємо лему, тоді з рівності (3) маємо
 Отже Теорему Крамера доведено. Векторний простір Подальше вивчення векторного простору. У довільному векторному просторі означення лінійно залежних і лінійно незалежних систем векторів, а тому і максимально лінійно незалежних систем і базису, переносяться один до одного з геометричного простору. В цьому курсі розглядаються лінійні простори, базиси яких містять скінчену кількість векторів. Теорема. Будь-який вектор лінійного(векторного) простору єдиним чином розкладається за базисом. Доведення. Нехай задано довільний векторний простір V і його базис
1. Доведення можливості розкладання. Розглянемо систему Припустимо, що Це означає, що вектори базису лінійно залежні, що суперечить означенню. Отже s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:lang w:val="UK"/></w:rPr><m:t>+1</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:lang w:val="UK"/></w:rPr><m:t>в‰ 0</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> З рівності випливає можливість доведення, адже:
2. Доведення єдиності розкладання. Припустимо, що існує вектор
Для визначеності нехай
Отже, ми отримали, що базисні вектори є лінійно залежними, що суперечить означенню базиса. Теорему доведено. Означення. Коефіцієнти розкладання вектора Вправа. Довести, що: |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 321. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

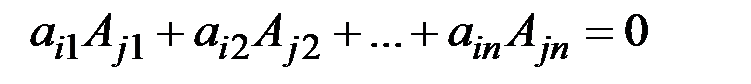
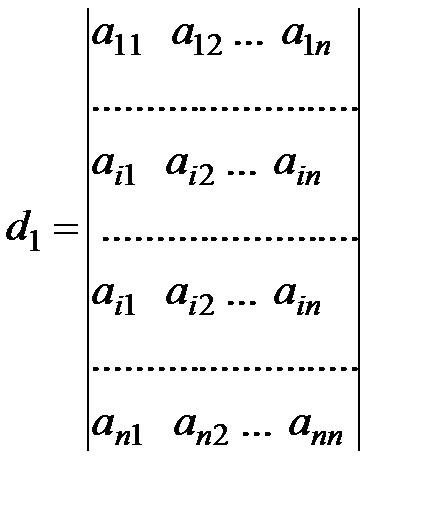
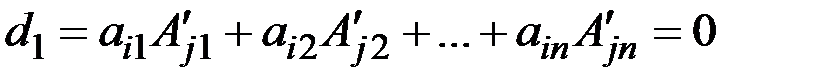
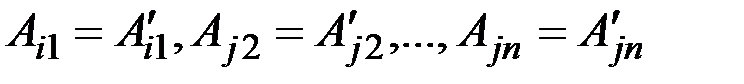 . Ці рівності випливають з того, що при побудові алгебраїчних доповнень до елементів j-го рядка цей рядок викреслюється, а визначники d і d1 відрізняються лише j-тим рядком.
. Ці рівності випливають з того, що при побудові алгебраїчних доповнень до елементів j-го рядка цей рядок викреслюється, а визначники d і d1 відрізняються лише j-тим рядком.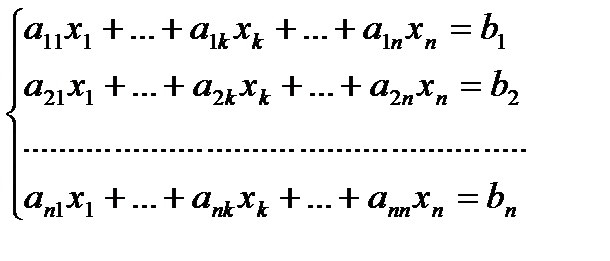 (1)
(1)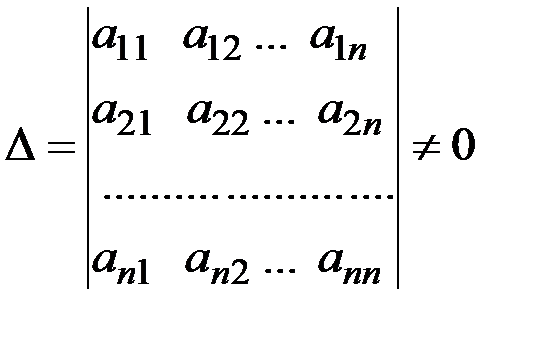 (2)
(2)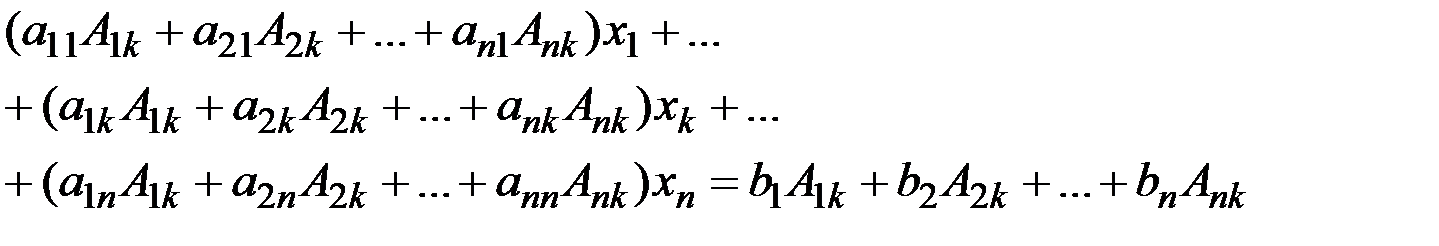
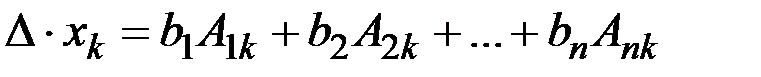 k=1,2,…,n (3)
k=1,2,…,n (3)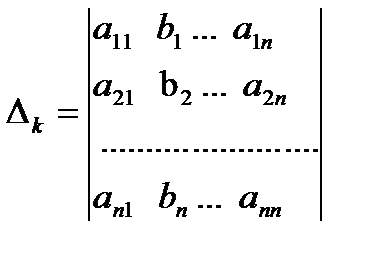
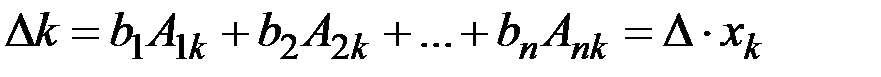
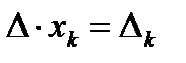
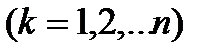
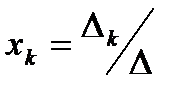
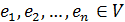 . Розглянемо довільний вектор
. Розглянемо довільний вектор 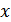 , що належить V.
, що належить V. – лінійно залежну за означенням базису. Тоді існують числа
– лінійно залежну за означенням базису. Тоді існують числа 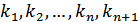 , серед яких
, серед яких 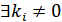 . Доведемо, що саме s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>+1</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:lang w:val="UK"/></w:rPr><m:t>в‰ 0</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
. Доведемо, що саме s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>+1</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:lang w:val="UK"/></w:rPr><m:t>в‰ 0</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 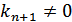 .
.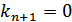 . Тоді
. Тоді 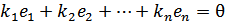 .
.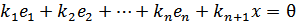 .
.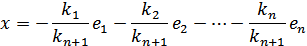
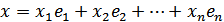 (1)
(1)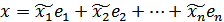 (2)
(2)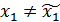 . Помножимо рівність (2) на -1 і додамо до (1).
. Помножимо рівність (2) на -1 і додамо до (1).