
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Зв’язок між розв’язком неоднорідної і відповідної однорідної системи рівнянь.Нехай задано неоднорідну систему Означення. Відповідною однорідною системою називається система з тими ж самими коефіцієнтами Звя’язок між розв’язками системи (1) та (2) описується наступними теоремами. Теорема 1. Сума розв’язків неоднорідної і відповідної однорідної системи лінійних алгебраїчних рівнянь є розв’язком неоднорідної системи . Теорема 2.Різниця двох розв’язків неоднорідної системи є розв’язком відповідної однорідної системи. Доведення теореми 1. Нехай ( За означенням розв’язку маємо систему правильних числових рівностей Підставимо в ліву частину системи (1) замість Перша властивість доведена.
Доведення теореми 2. Нехай ( За означенням розв’язку маємо системи правильних числових рівностей: Підставимо в ліву частину рівнянь системи (2) замість  Таким чином , одержуємо Твердження.З цих двох теорем випливає такий алгоритм розв’язування неоднорідної системи рівнянь : множину всіх розв’язків можна одержати додавання до кожного розв’язку множини розв’язків однорідної системи одного розв’язку (окремого) неоднорідної системи. Доведенння твердження. Нехай Н=
Нехай Розглянемо суму Виникає питання, може система (1) має інші розв’язки, що отримуються за іншим алгоритмом ? Доведемо, що цього не може бути. 2) Нехай Алгебра матриць
Розглянемо спочатку квадратні матриці одного і того ж n- го порядку. Для матриць введено три операції : 1) множиння матриць; 2) додавання матриць; 3) множиння матриці на число. Множиння матриць. Означення. Добутком матриць А і В називається матриця С того ж самого порядку, що матриці А та В, елементи якої утворюються за таким законом: елемент А= Закони множення. 1. Множення матриць, взагалі кажучі, не комутативне. Для того, щоб в цьому переконатись,досить знайти дві матриці А і В, для яких А×В ¹ В×А . А= А×В =
В×А = З наведеного прикладу бачимо, що А×В ¹ В×А . При цьому ми виходили з такого означення рівних матриць. Означення.Матриці А і В називаються рівними, якщо на одних і тих самих місцях знаходяться рівні елементи. Теорема . Множення матриць підпорядковується асоціативному закону. Тобто ми повинні довести, що для будь-яких матриць А, В і С має місце рівність ( А × В ) × С = А × ( В × С ) . Нехай А=(
( А × В ) × С = C ×D = F ( А × (В × С ) = А× Р = Т ( В цих позначеннях треба довести, що F = Т , тобто Обчислимо Підставимо (2) в (1) , отримаємо Преходимо до обчислення Підставимо (5) в (4), отримаємо
Порівнюючи (3) і (6), приходимо до висавку, що Хоча множення матриць, взагалі кажучі, некомутативне, існує матриця, яка комутує з будь-якою матрицею А, і більш того, в добутку з даною матрицею не змінює цю матрицю А. Це так звана одинична матриця : Е = Ця матриця має такі властивості : 1) А × Е = А , " А 2) Е × А = А , " А , а звідси випливає, що А × Е = Е × А . Доведемо другу властивість.
Е × А =
=
Так само доводиться перша властивість, тобто безпосереднім множенням. Теорема. Доведеня.Нехай задано матриці А і В , а С – добуток цих матриць. Треба довести, що det C = det A ×det B . Для доведення побудуємо визначник d порядку 2n :
d =
Застосуємо до перших n рядків цього визначника теорему Лапласа d = det A ×det B ( d = det A ×det B (1) Перетворимо визначник d за допомогою восьмої властивості визначників. До (n+1) стовпчика додамо перший стовпець помножений на Аналогічно зробимо з (n+2)-им стовпцем, (2n)-им стовпцем. В правому нижньому куті отримаємо нульовий блок порядку n. А правий верхній кут, тоді перетворюється в елементи матриці С.
Застосуємо до цього визначника теорему Лапласа . d = det C Користуючись формулою суми 2n членів арифметичної прогресії, маємо d = det C Вправа. Довести самостійно єдиність одиничної матриці (скористатись методикою доведення єдиності нульового вектора будь-якого лінійного простору). |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 357. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
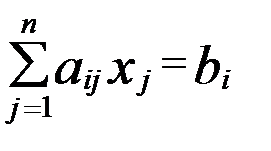 ,
, 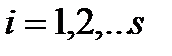 (1)
(1)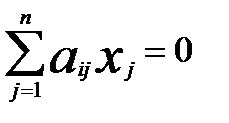 ,
, 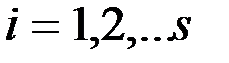 (2)
(2)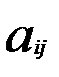 .
.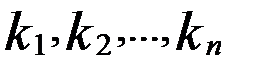 ) – розв’язок системи (1), (
) – розв’язок системи (1), ( 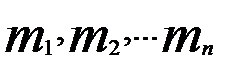 ) – розв’язок системи (2). Треба довести , що
) – розв’язок системи (2). Треба довести , що 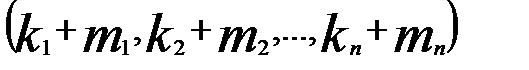 - розв’язок системи (1) .
- розв’язок системи (1) .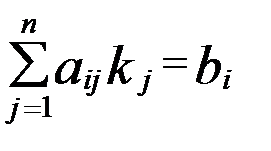 , (
, ( 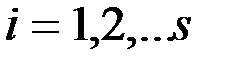 ) (3)
) (3)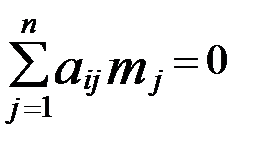 , (
, ( 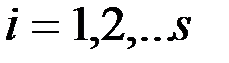 ) (4)
) (4)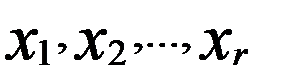
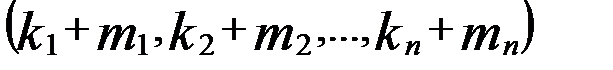 .
.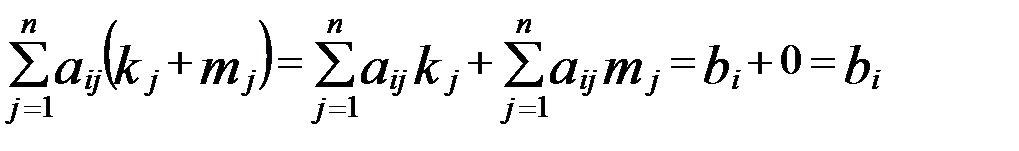
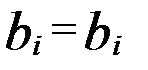 (
( 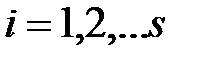 )
)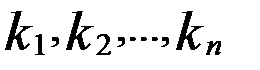 ) , (
) , ( 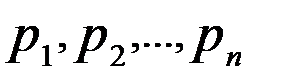 ) – розв’язки системи (1). Розглянемо упорядкований набір
) – розв’язки системи (1). Розглянемо упорядкований набір 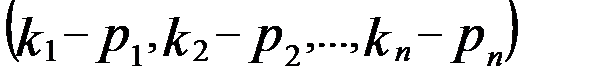 . Ми повинні довести, що це розв’язок системи (2) .
. Ми повинні довести, що це розв’язок системи (2) .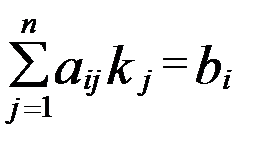 , (
, ( 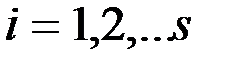 ), (3)
), (3)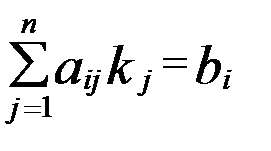 , (
, ( 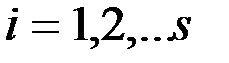 ). (3’)
). (3’)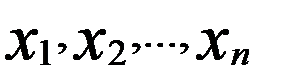 числа
числа 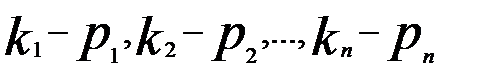 відповідно і обчислимо її.
відповідно і обчислимо її. .
. правильних числових рівностей.
правильних числових рівностей.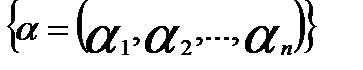 – множина розв’язків системи (1),
– множина розв’язків системи (1),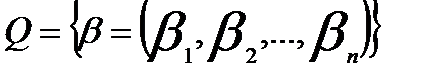 – множина розв’язків системи (2).
– множина розв’язків системи (2).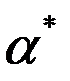 - окремий розв’язок системи (1).
- окремий розв’язок системи (1).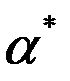 з будь-яким розв’язком однорідної системи.
з будь-яким розв’язком однорідної системи.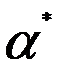 +
+ 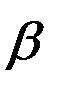 =
= 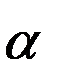 ** є Н - розв’язок системи (1) .
** є Н - розв’язок системи (1) .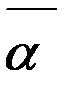 є Н. Доведемо, що
є Н. Доведемо, що 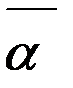 можна одержати додаванням до
можна одержати додаванням до 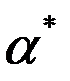 якогось розв’язку з множини Q . Розглянемо різницю (
якогось розв’язку з множини Q . Розглянемо різницю ( 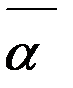 -
- 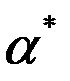 ). Тоді за теоремою 2 , це розв’язок системи (2), тобто (
). Тоді за теоремою 2 , це розв’язок системи (2), тобто ( 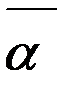 -
- 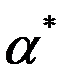 ) =
) = 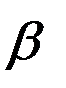 * є Q. Отже
* є Q. Отже 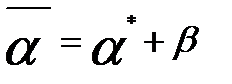 .
.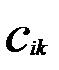 розташованний в і-тому рядку та к-му стовпцю матриці С дорівнює сумі добутків елементів і-того рядка матриці А на відповідні елементти к-того стовпця матриці В.
розташованний в і-тому рядку та к-му стовпцю матриці С дорівнює сумі добутків елементів і-того рядка матриці А на відповідні елементти к-того стовпця матриці В.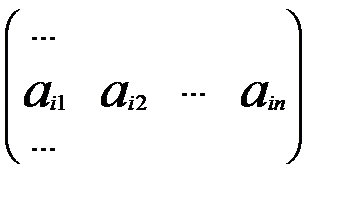 , В=
, В= 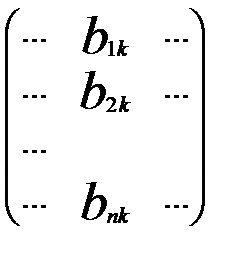
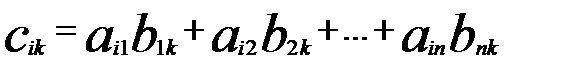 .
.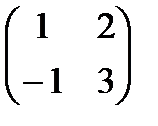 , В=
, В= 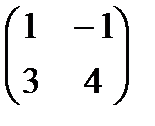 .
.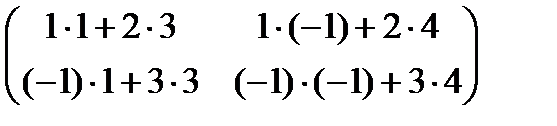 =
= 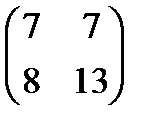 ,
,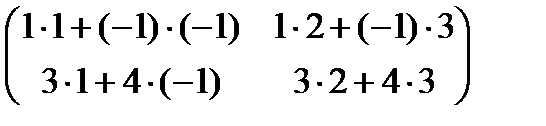 =
= 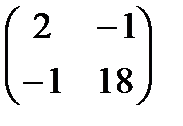 .
.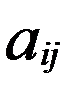 ) , В=(
) , В=( 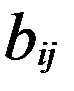 ) . А × В = D = (
) . А × В = D = ( 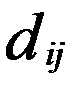 )
) 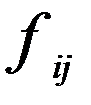 ) , ( В × С ) = Р (
) , ( В × С ) = Р ( 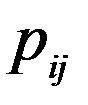 )
) 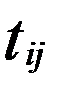 ) .
) .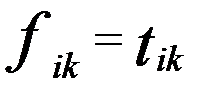 (
( 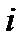 = 1,2,…,
= 1,2,…, 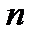 )
)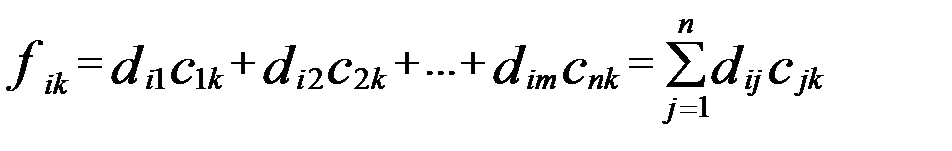 , (1)
, (1)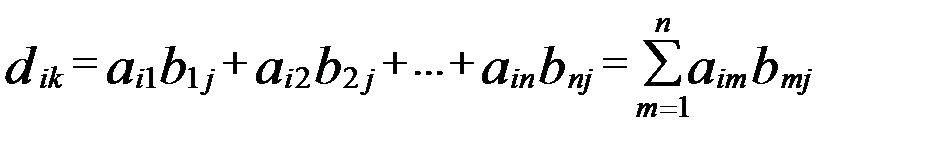 , (2)
, (2)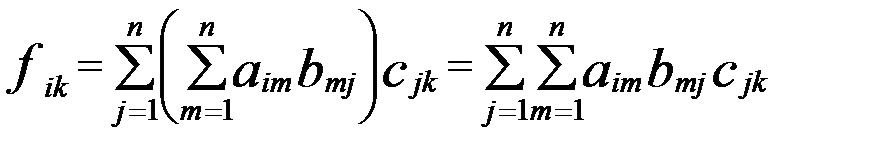 (3)
(3)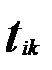 .
.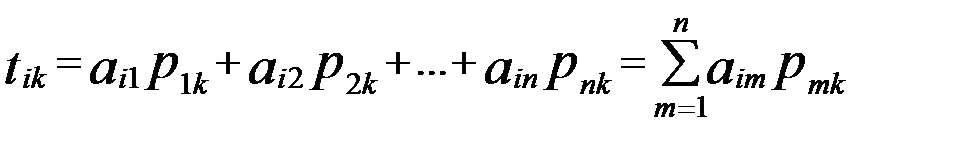 (4)
(4)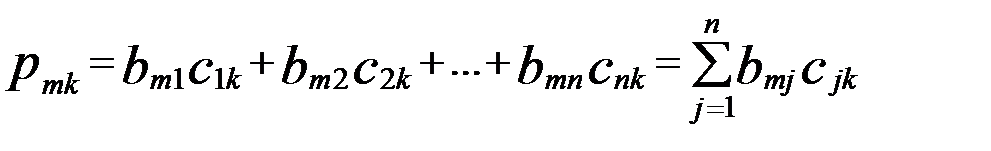 (5)
(5)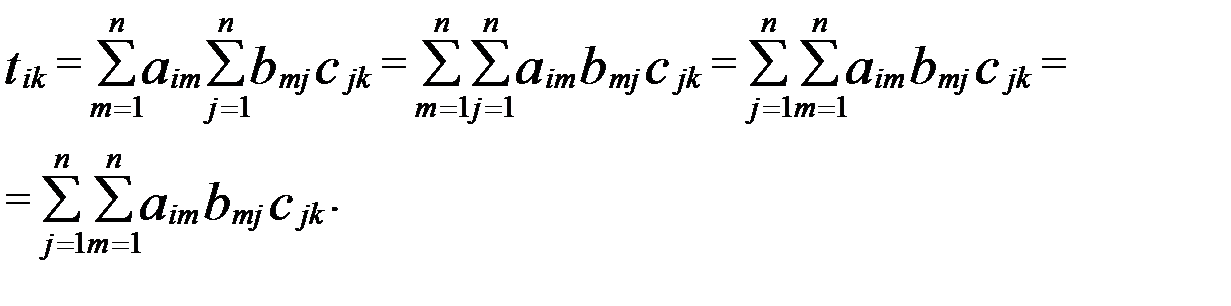 (6)
(6)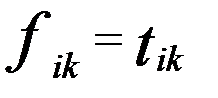 , що й треба було довести .
, що й треба було довести .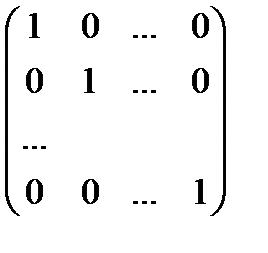 .
.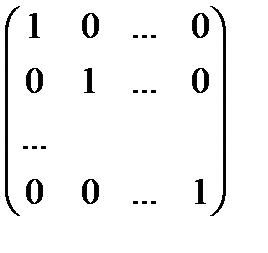 ×
× 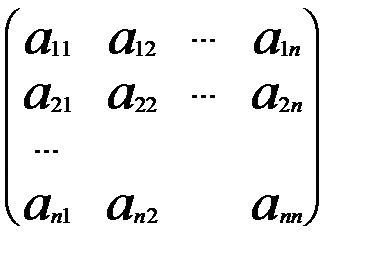 =
= 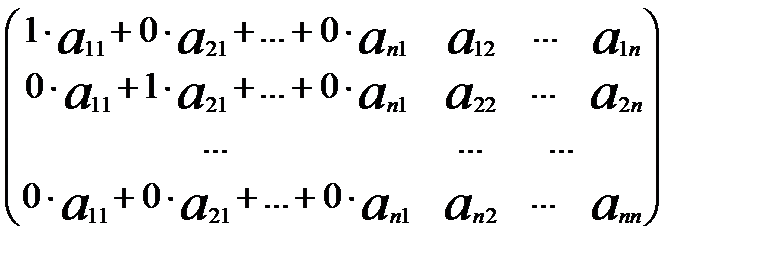 = А .
= А .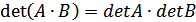 .
.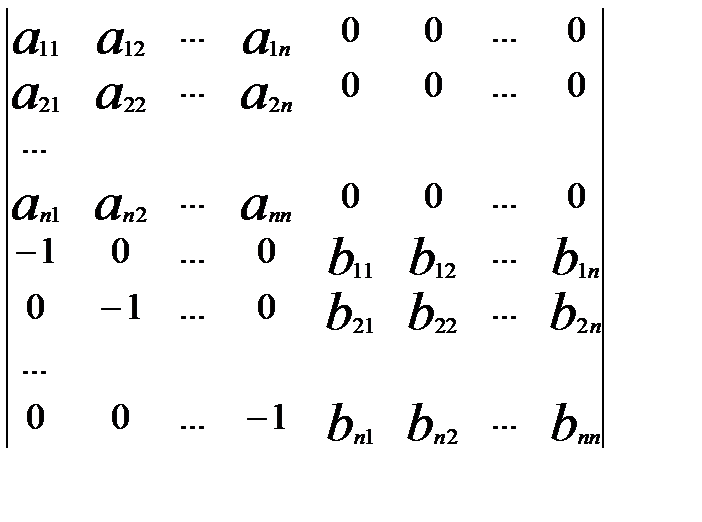 .
.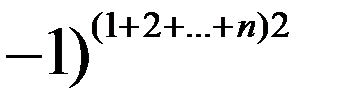 , тобто
, тобто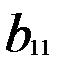 , другий – на
, другий – на 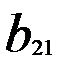 , n-ий – на
, n-ий – на 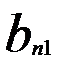 .
.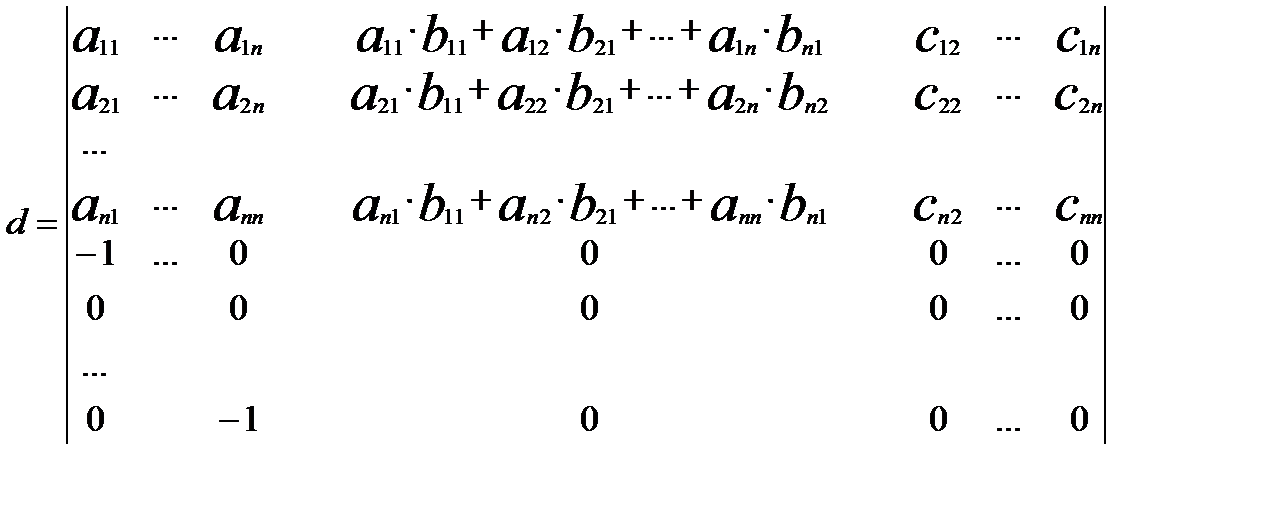

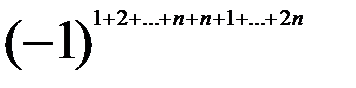 .
.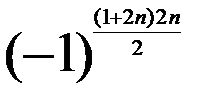 , det C = det A × det B .
, det C = det A × det B .