
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Матриці обернені до даних. Умови їх існування.Внаслідок того, що множення матриць, взагалі кажучі, не комутативне, в цьому питанні слід розглядати ліві обернені матриці праві. Означення. Матриця, що умовно позначається Означення. Матриця, що умовно позначається Для з’ясування умов існування обернених матриць введемо поняття невироджених (неособливих) і вироджених (особливих) матриць. Означення. Квадратна матриця називається невиродженою, якщо її визначник не дорівнює нулю. В противному разі квадратна матриця називається виродженою. Теорема 1.Жодна вироджена матриця не має ні лівої оберненої, ні правої оберненої матриці. Доведення. Нехай задана матриця А, det A = 0. Треба довести, що не існує ні правої оберненої, ні лівої оберненої матриці. Припустимо, що існує хоча б одна з них. Нехай існує ліва обернена матриця. Тоді det E = det 1 = 0, отримали суперечність. Таким чином, не існує Теорему доведено. Теорема 2.Для будь-якої невиродженої матриці існує і ліва обернена, і права обернена, і вони рівні . Доведення.Нехай задано матрицю А. причому det A = d Треба довести, що існує ліва обернена , права обернена матриці, та

Доведемо, що 1) А 2) Доведемо 1) Застосувавши правило множення, лему до теореми Крамера і наслідок з теореми Лапласа маємо: А ×
Так само, безпосереднім множенням матриць доводиться друга рівність. З першого пункта випливає
Отже ми довели існування оберненої матриці та її обчислення: Вправа. Довести єдиність матриці |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 280. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , називається лівою оберненою до матриці А, якщо вона задовольняє умову
, називається лівою оберненою до матриці А, якщо вона задовольняє умову 
 .
. , називається правою оберненою до матриці А, якщо вона задовольняє умову
, називається правою оберненою до матриці А, якщо вона задовольняє умову 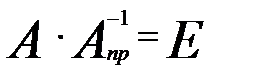 .
. (з означення). Застосуємо теорему про визначник добутку матриць:
(з означення). Застосуємо теорему про визначник добутку матриць: . det A ,
. det A , , так само доводиться, що не існує
, так само доводиться, що не існує  .
.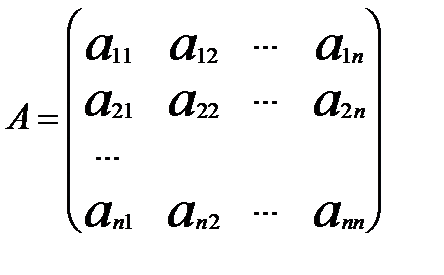 ,
, 0 .
0 . =
=  . З матриці А побудуємо матрицю
. З матриці А побудуємо матрицю  , заміною кожного елемента aij його алгебраїчним доповненням Аij і протранспонувавши отримаємо матрицю:
, заміною кожного елемента aij його алгебраїчним доповненням Аij і протранспонувавши отримаємо матрицю: =
= 
 .
. = Е ;
= Е ; А = Е .
А = Е . =
= 
 =
= =
=  .
.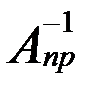 , а з другого пункту
, а з другого пункту  .
.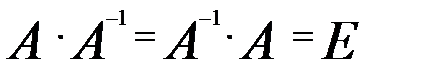 .
. =
=  .
.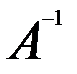 (Доведення проводиться за схемою доведення єдиності протилежного вектора).
(Доведення проводиться за схемою доведення єдиності протилежного вектора).