
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Координати вектора суми двох векторів дорівнюють сумі відповідних координат.Координати добутку вектора на число можна отримати множенням його координат на це число. Означення. Лінійний простір називається n-вимірним, якщо в ньому існує n лінійно незалежних векторів, а будь-яка система з n+1 вектора лінійно залежна. З'ясуємо вимірність арифметичного простору. Доведемо таку теорему. Теорема. При
арифметичного простору лінійно залежна. Доведення. Розглянемо рівність (*) з означення лінійно залежної і лінійно незалежної системи:
З'ясуємо, при яких
З цієї векторної рівності отримаємо п-числових різностей.
Отримали систему n-рівнянь з s-невідомими. Ця система завжди сумісна тому що вона має принаймні один нульовий розв'язок. Але за допомогою елементарних перетворень вона зводиться до кінцевого вигляду, де кількість рівнянь менша за кількість невідомих. Повертаючись до рівності (*) приходимо до висновку що рівність (*) виконується коли принаймі одне з Наслідок.Будь-яка система з n + 1 вектора з п-компонентами є лінійно-залежна. Це негайно випливає, якщо з покласти З цього випливає, що вимірність арифметичного простору не більш ніж: п. Для того, щоб довести, що вимірність дорівнює n треба знайти принаймні одну лінійно незалежну систему векторів, що містить n-векторів. Такою системою векторів є наприклад:
Доведемо, що вони лінійно незалежні. Складемо рівність (*).
З цього випливає
Тобто (*) виконується лише один раз при Отже, ми довели, що арифметичний простір є n-вимірним (n – кількість компонент вектора).  Зауваження. Поняття вимірності лінійного простору можна ввести і за таким означенням. Означення. Вимірністю лінійного простору називається кількість векторів, що входять до базису. Для того щоб це означення було корректним треба було б довести, що усі базиси даного простору містять однакову кількість векторів (насправді, це так). Позначимо n-вимірний довільний векторний простір через Vn. Введемо поняття підпростору даного простору Vn. Означення. Підмножина Безпосередньо з означення лінійного простору випливає, що для того щоб переконатися, що підмножина Доведемо це. Нехай в Якщо а) б) Зрозуміло, оскільки всі елементи множини Доведемо, що виконується умова – аксіома 3), 4), тобто що |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 336. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 система векторів
система векторів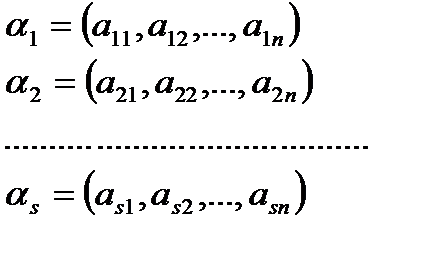
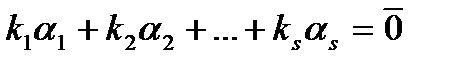
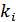 вона виконується:
вона виконується:
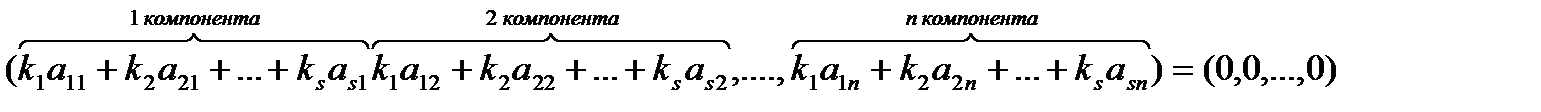
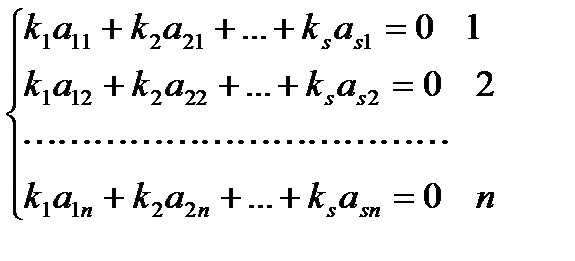
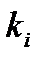 -тих не дорівнює нулю, тому
-тих не дорівнює нулю, тому 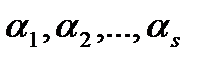 -лінійно залежні.
-лінійно залежні.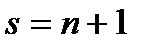 .
.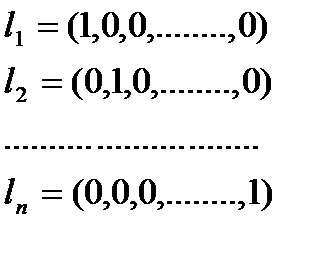
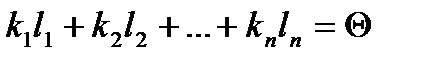 (*)
(*)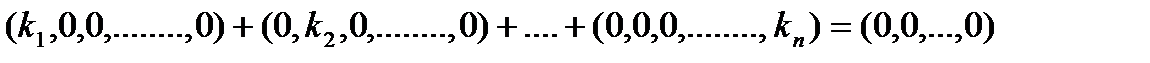
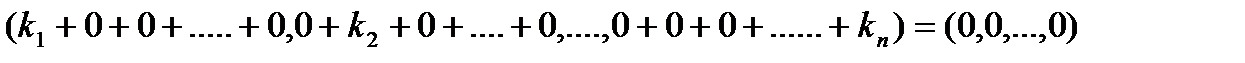
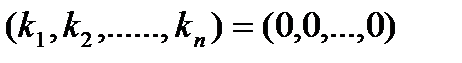
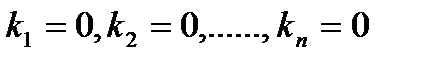
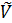 лінійного простору Vn називається підпростором даного простору, якщо
лінійного простору Vn називається підпростором даного простору, якщо 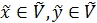 ,то
,то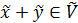 ;
;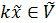 .
.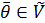 . Наспправді, нехай
. Наспправді, нехай 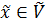 , оскільки
, оскільки 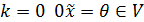 , а при
, а при 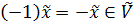 .
.