
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
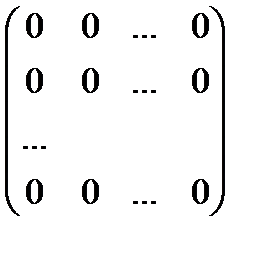
Операції додавання і множення на число.Означення. Сумою матриць А і В , А=( D = ( Означення. Добутком матриці А на число k , називається матриця F, елементи якої обчислюються за законом F = (k Введені операції мають такі властивості : 1) А + В = В + А ; 2) (А + В)+С = А+(В + С) ; 3) $ Q : А + Q = А + Q + А ; Q = 4) " А $ (-А) : А + (-А) = (-А) + А = 0. Вона і снує , тому що є (-А) = (- 5) А = А ; 6) k (l A) = (k l) A ; 7) k (A + B) = kA + kB ; 8) (k + l) A = kA + lA : Перевірити самостійно. Таким чином, множина всіх матриць є векторним простором, більш того, арифметичним, вимірності Розглянемо хоча б один базіс цього простору. Це так звані матриці Таких матриць існує n2.
Доведемо, що це базис. Доведемо, що це лінійно незалежні матриці. Для цього з’ясуємо, при яких kij виконується рівність
Отже рівність (*) виконується лише в нульовому випадку усіх kij, тому матриці лінійно залежні. З того, що вимерність простору матриць дорівнює Розглянемо довільну матрицю А. Доведемо, що А = Введемо в розгляд допоміжну матрицю:
Доведемо, що цю матрицю можна подати у вигляді Насправді
Розглянемо тепер матрицю А. Її можна подати у вигляді
Застосуємо до кожного доданку попередню формулу
Вправа. Довести, що операція множення матриць і додавання матриць підпорядковується дистрибутивному закону :  А (В + С) = АВ + ВС .
Доведення. Необхідність. Нехай матриця С є скалярною. Треба довести, що С = Вище було доведено, що така матриця комутує з будь-якою матрицею А. Таким чином, необхідність доведена. Достатність. Нехай деяка матриця С загального вигляду С = комутує з будь-якою матрицею А . Треба довести, що матриця С – скалярна матриця, тобто З того, що
Матриці (1), (2) за умовою теореми рівні, тому що на однакових місцях повинні знаходитись рівні елементи. Порівняємо елементи i-тих рядків ицх матриць. 0 = Таким чином, ми одержали, що матриця С має діагональні елементи рівними, а елементи позадіагональні є нульовими, тобто матриця С – скалярна матриця.
Скалярні матриці. Означення. Скалярною матрицею називається матриця вигляду До класу скалярних матриць належить одинична матриця, а також нульова. Позначимо k × Е = Доведемо, що кЕ комутує з будь-якою матрицею (к Е) А = А (к Е ) , Безпосереднім множенням матриць, переконуємося 1) ( к Е ) А = 2) А ( к Е ) =
Звідси випливає, що скалярна матриця комутує в добутку з будь-якою матрицею А. Насправді справедливе і обернене. А тому має місце така теорема. Теорема. Для того, щоб матриця була скалярною, необхідно і достатньо, щоб вона комутувала з будь-якою матрицею .
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 296. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ) , В=(
) , В=(  ) , називається матриця D, елементи якої обчислюються за законом
) , називається матриця D, елементи якої обчислюються за законом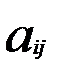 +
+  ).
). ) .
) . .
. ) .
) . .
.  .
. =
=  .
. ,
, 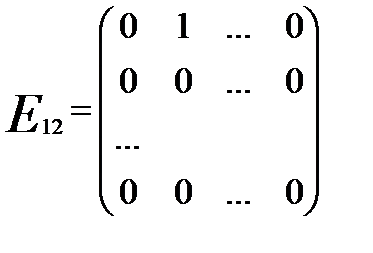 , … ,
, … ,  ,
, ,
,  , … ,
, … , 
 (*)
(*) = 0 .
= 0 .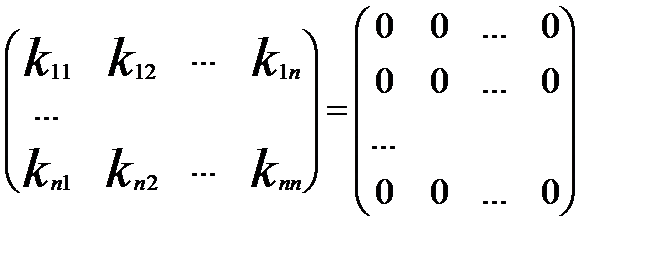 ,
, 
 .
. , випливає, що матриці
, випливає, що матриці  утворюють базіс. Тоді будь-яка матриця А повинна бути лінійною комбінацією матриць
утворюють базіс. Тоді будь-яка матриця А повинна бути лінійною комбінацією матриць  . Знайдемо цю лінійну комбнацію.
. Знайдемо цю лінійну комбнацію. .
. .
. .
.


 , " А. З того, що матриця С скалярна, вона має вигляд
, " А. З того, що матриця С скалярна, вона має вигляд
 .
. ,
, ,
, 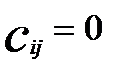 , якщо i ¹ j .
, якщо i ¹ j . .
.
 (1)
(1)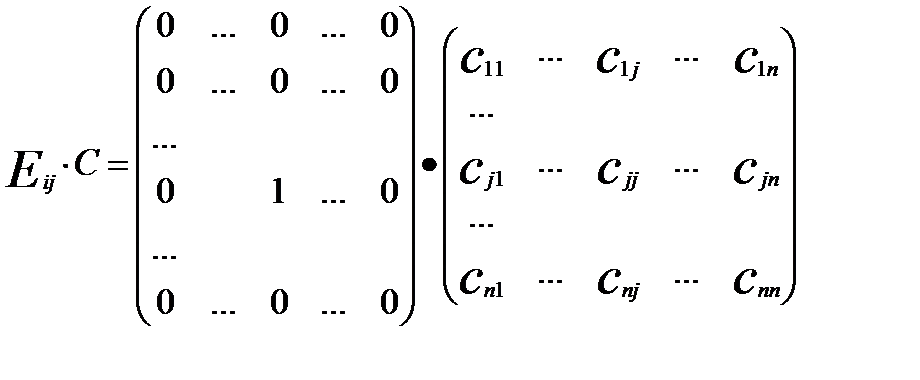 .
. (2)
(2) , 0 =
, 0 =  , … ,
, … ,  , 0 =
, 0 = 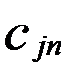
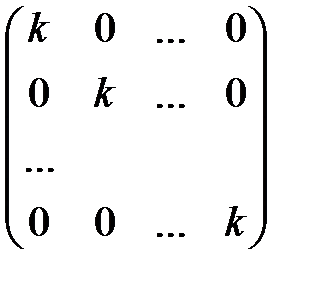 .
. .
. А .
А . .
. .
.