
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Загальна теорія лінійно-алгебраїчних рівняньКритерій сумісності лінійних алгебраїчних рівнянь Теорема Кронекера-Капеллі. Для того, щоб система лінійних алгебраїчних рівнянь була сумісною, необхідно і достатньо, щоб ранг матриці системи дорівнював рангу розширенної матриці.
Означення. Матрицею системи називають матрицю утворену з коефіціентів при невідомих. Розширеною матрицею називають матрицю системи, яка утворена з матриці системи приєднанням стовпця вільних членів.
Доведення теореми.Нехай задана система
Необхідність. Нехай система (1) сумісна. Треба довести, що r A = r` За означенням розв'язку маємо систему правильних числових рівностей
Ці рівності означають, що останній стовпець матриці ` Достатність. Нехай r A = r A . Треба довести, що система (1) сумісна. Тоді будь-яка максимальна лінійно незалежна система стовпців матриці А залишається максимально лінійно незалежною системою і в матриці `А. Таким чином, через цю систему, а тому і взагалі через систему стовпців матриці А, лінійно виражається останній стовбець матриці А. Отже, існує така система коефіцієнтів 
Критерій визначеності і невизначеності системи Теорема. 1. Якщо ранг матриці А дорівнює рангу розширеної матриіці 2. Якщо ранг матриці А дорівнює рангу розширеної матриіці Доведення.Нехай задано систему
За умовою rA=r
Рівність рангів означає, що в матриці В отриманій системі ліворуч запишемо ті невідомі, коефіцієнти при яких утворюютъ визначник р-того порядку, не рівний нулю. За нашим припущенням це перші р. Отже, отримаемо систему
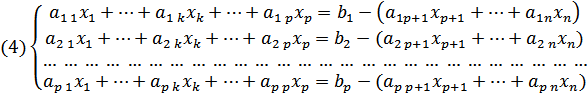 . .
Будемо розглядати цю систему, як систему р рівнянъ з р невідомими і з визначником, що не дорівнює нулю. Застосуємо теорему Крамера. Тоді матимемо для
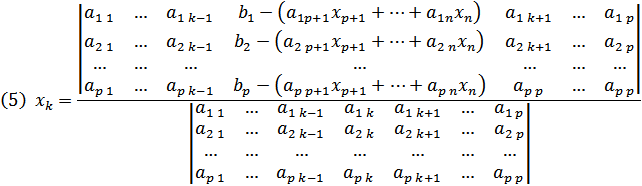
Розглянемо два випадки. 1) Нехай p<n. Тоді існують вільні невідомі 2) Нехай p=n. Покладемо в (5)
Тобто в цьому випадку вільних невідомих система не має, тому система має один розв’язок , а тому є визначеною. З формули (5) отримаємо співвідношення (**) для однорідної системи, важливе для наступного розділу. Означення. Однорідною системою лінійних алгебраїчних рівнянь називається лінійна система, вільні члени якої дорівнюють нулю. Запишемо формулу (5) для однорідної системи:
Розкладемо цей визначник за елементами k-того стовбця
Розкриємо всі дужки, зведемо подібні, тоді отримаємо:
|
||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 339. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
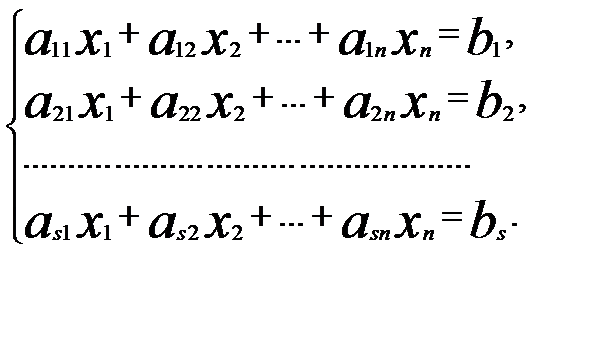 (1)
(1)
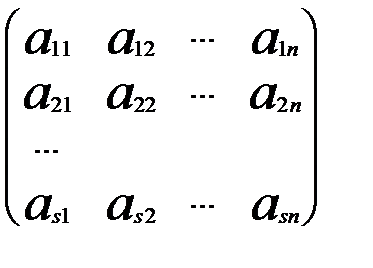
 ,
, 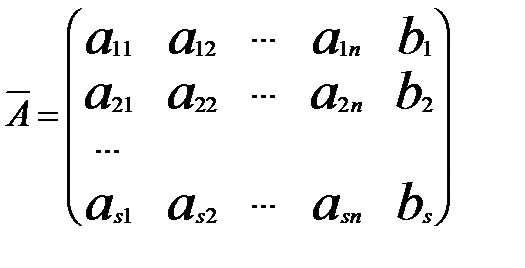 .
.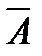 . Скористаємось умовою, що система (1) сумісна: Нехай (
. Скористаємось умовою, що система (1) сумісна: Нехай ( 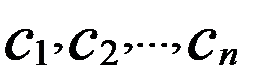 ) – розв’язок системи (1).
) – розв’язок системи (1).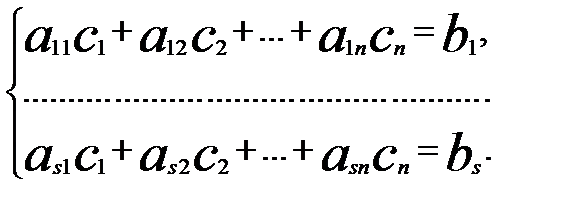
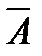 є лінійною комбінацією стовпців матриці А. З цього випливає, що максимальна кількість стовців матриці А збігається з максимальною кількістю стовпців матриці `А , тобто r A = r`A.
є лінійною комбінацією стовпців матриці А. З цього випливає, що максимальна кількість стовців матриці А збігається з максимальною кількістю стовпців матриці `А , тобто r A = r`A.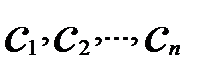 , що сума стовпців матриці А, взятих з цими коефіцієнтами, дорівнює стовпцю з вільних членів, а тому числа
, що сума стовпців матриці А, взятих з цими коефіцієнтами, дорівнює стовпцю з вільних членів, а тому числа 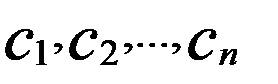 є розв’язком системи (1). Таким чином, якщо r A = r
є розв’язком системи (1). Таким чином, якщо r A = r 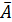 і це спільне значення менше n (rA=r
і це спільне значення менше n (rA=r 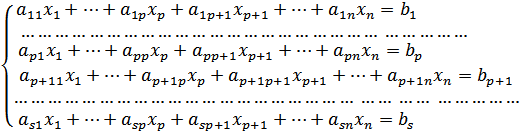


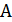 і
і 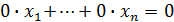 , отже їх можна відкинути.
, отже їх можна відкинути.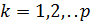 :
: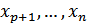 в тому сенсі, що їх можна задавати довільно. Тобто, в цьому випадку система має безліч розв’язків, а тому є невизначеною.
в тому сенсі, що їх можна задавати довільно. Тобто, в цьому випадку система має безліч розв’язків, а тому є невизначеною.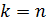 :
: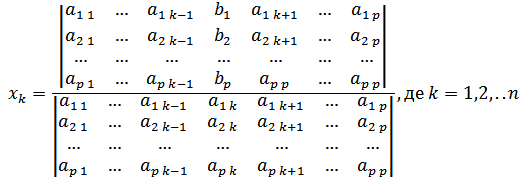
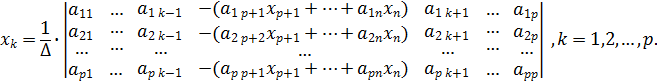
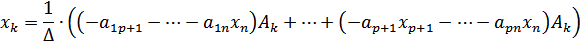
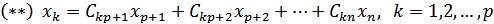 .
.