
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пропорциональном скорости (затухающие колебания)Рассмотрим, как влияет на свободные колебания сопротивление среды, приняв, что сила сопротивления пропорциональна первой степени скорости:
Дифференциальное уравнение примет вид
Рис. 3.12
Деля обе части на m, получим:
где обозначено
Уравнение (3.38) представляет собой дифференциальное уравнение или по аналогии с равенством (3.30)
Входящие в (3.41) постоянные являются постоянными интегрирования и определяются по начальным условиям. Колебания, проходящие по закону (3.38), называют затухающими (рис. 3.13), так как благодаря множителю Промежуток времени
принято называть периодом затухающих колебаний.
Рис. 3.13
Формулу (3.42), если учесть равенство (3.35), можно представить в виде
Из формул (3.42) и (3.42/) видно, что наличие сопротивления увеличивает период колебаний. Однако, когда сопротивление мало
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 379. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 («–» указывает, что R противоположна v). Пусть на точку при её движении действует восстанавливающая сила
(«–» указывает, что R противоположна v). Пусть на точку при её движении действует восстанавливающая сила 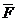 и сила сопротивления
и сила сопротивления 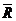 (рис. 3.12). Тогда
(рис. 3.12). Тогда
 .
. .
.
 , (3.38)
, (3.38) ,
,  . (3.39)
. (3.39) (3.40)
(3.40) . (3.41)
. (3.41) величина
величина  с течением времени убывает, стремясь к нулю.
с течением времени убывает, стремясь к нулю. , равный периоду
, равный периоду  , т. е. величину
, т. е. величину , (3.42)
, (3.42)
 . (3.42/)
. (3.42/) , то величиной
, то величиной  по сравнению с единицей можно пренебречь и считать
по сравнению с единицей можно пренебречь и считать  .
.