
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИИ ИХ ИНТЕГРИРОВАНИЕ Прямолинейное движение точки Из кинематики известно, что при прямолинейном движении скорость и ускорение точки все время направлены вдоль одной и той же прямой. Так как направление ускорения совпадает с направлением действия силы, то отсюда следует, что свободная материальная точка будет двигаться прямолинейно тогда, когда действующая на нее сила имеет постоянное направление, а скорость точки в начальный момент равна нулю или направлена вдоль силы. Рассмотрим материальную точку, движущуюся прямолинейно под действием приложенной к ней силы Положение точки на траектории определяется ее координатой х Связь между х и R дает уравнение (3.3). Проектируя обе его части
Так как Уравнение (3.6) называется дифференциальным уравнением прямолинейного движения точки.
Рис. 3.1
Часто уравнение (3.6) бывает удобнее заменить двумя дифференциальными уравнениями, содержащими первые производные: В тех случаях, когда при решении задачи надо искать зависимость скорости от координаты х, а не от времени t (когда сами силы зависят от х), уравнение (3.7) преобразуют к переменному х. Так как  Решение основной задачи динамики сводится к тому, чтобы из данных уравнений, зная силы, найти закон движения, т. е. Входящие в уравнение (3.6) силы могут зависеть от времени t, положения точки, т. е. х и ее скорости, т. е. После того как с помощью тех или иных математических приемов уравнение (3.9) будет проинтегрировано, в полученное решение войдут две постоянные интегрирования С1 и С2, и общее решение будет иметь вид Постоянные С1 и С2 определяют, используя начальные условия.
Криволинейное движение точки Рассмотрим свободную материальную точку, движущуюся под действием сил Проведем неподвижные координатные оси О, х, у, z; проектируя на них обе части равенства
Рис. 3.2
Так как действующие на точку силы могут зависеть от времени, положения точки и скорости, то по аналогии с (3.9) правые части уравнения (3.11) могут содержать время t, координаты точки х, у, z и проекции ее скорости
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 414. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
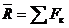 .
.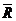 , найти закон движения точки, т. е.
, найти закон движения точки, т. е. 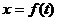 .
.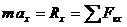 .
.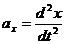 , то
, то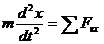 (3.6)
(3.6)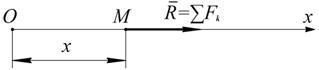
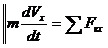 (3.7)
(3.7)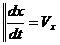 (3.7/)
(3.7/)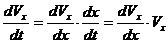 , то
, то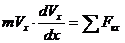 . (3.8)
. (3.8)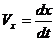 . Следовательно, в общем случае уравнение (3.6) с математической точки зрения представляет дифференциальное уравнение второго порядка.
. Следовательно, в общем случае уравнение (3.6) с математической точки зрения представляет дифференциальное уравнение второго порядка.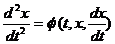 . (3.9)
. (3.9)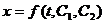 . (3.10)
. (3.10)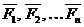 (рис. 3.2).
(рис. 3.2).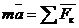 и учитывая, что
и учитывая, что 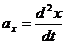 и т. д., получим дифференциальные уравнения криволинейного движения точки:
и т. д., получим дифференциальные уравнения криволинейного движения точки: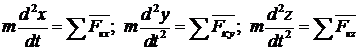 . (3.11)
. (3.11)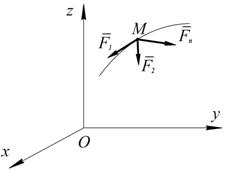
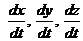 . Уравнения (3.11) позволяют решать как первую, так и вторую основную задачи динамики. Чтобы с помощью них решать основную задачу динамики, кроме действующих сил, надо знать начальные условия, т. е. положение и скорость точки в начальный момент. В координатных осях О, х, у, z начальные условия задаются в следующем виде: при t = 0
. Уравнения (3.11) позволяют решать как первую, так и вторую основную задачи динамики. Чтобы с помощью них решать основную задачу динамики, кроме действующих сил, надо знать начальные условия, т. е. положение и скорость точки в начальный момент. В координатных осях О, х, у, z начальные условия задаются в следующем виде: при t = 0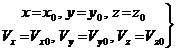 (3.12)
(3.12)