
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема об изменении количества движенияРассмотрим систему, состоящую из n материальных точек, составим для нее дифференциальные уравнения движения (4.2) и сложим их почленно:
По свойству внутренних сил
Окончательно находим: Уравнение (4.9) выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил. В проекциях на координате оси будем иметь:
Найдем другое выражение теоремы. Пусть в момент t = 0 количество движения равно или Уравнение (4.11) выражает теорему об изменении количества движения системы: изменение количества движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени. В проекциях на координатные оси
Закон сохранения количества движения Из теоремы об изменении количества движения системы можно получить важные следствия. 1. Пусть сумма всех внешних сил, действующих на систему, равна нулю: тогда из уравнения (4.8) следует, что при этом Таким образом, если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению.  2. Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например Ох) равна нулю: Тогда из уравнения (4.12) следует, что при этом Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения системы на эту ось есть величина постоянная. Эти результаты выражают закон сохранения количества движения системы, из которого следует, что внутренние силы изменить суммарное количество движения системы не могут. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 366. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. . Кроме того,
. Кроме того, .
.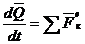 . (4.9)
. (4.9) (4.10)
(4.10) 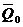 , а в момент t1 –
, а в момент t1 –  . Тогда, умножая обе части равенства (4.9) на dt и интегрируя, получим:
. Тогда, умножая обе части равенства (4.9) на dt и интегрируя, получим:
 . (4.11)
. (4.11)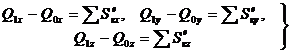 (4.12)
(4.12) ,
, .
. .
.