
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Количество движения и кинетическая энергия точкиКоличество движения и кинетическая энергия точки – это основные динамические характеристики движения. Количеством движения точки называется векторная величина Кинематической энергией (или живой силой) точки называется скалярная величина – Единицы измерения: в системе СИ
в системе СГС
Импульс силы Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводим понятия об импульсе силы. Элементарным импульсом силы называется векторная величина Элементарный импульс направлен по линии действия силы. Импульс Следовательно, импульс силы за любой промежуток времени
Теорема об изменении количества движения точки Так как масса точки постоянна, а ее ускорение  Уравнение (3.16) выражает одновременно теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна геометрической сумме действующих на точку сил. Проинтегрируем это уравнение. Пусть точка массой m, движущаяся под действием силы Умножим обе части равенства (3.16) на В результате получим:
Согласно формуле (3.14) окончательно имеем:
Рис. 3.3
Уравнение (3.17) выражает теорему об изменении количества движения точки: изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех действующих на точку сил за этот промежуток времени. При решении задач вместо векторного уравнения (3.17) часто пользуются уравнениями в проекциях Работа силы. Мощность Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы. При этом работа характеризует действие силы, которое определяет изменение модуля скорости движущей точки. Введем понятие об элементарной работе силы на бесконечно малом перемещении dS (рис. 3.4). Элементарной работой силы F называется скалярная величина
где dS – бесконечно-малое перемещение.
Рис. 3.4
Если разложить силу F на составляющие Замечая Таким образом, элементарная работа силы равна проекции силы на направление перемещения точки, умноженное на элементарное перемещение dS, или элементарная работа силы равна произведению модуля силы на элементарное перемещение dS и косинус угла между направлениями силы и перемещения. Если Если Найдем аналитическое выражение элементарной работы, для этого F разложим по координатным осям. Элементарное перемещение (рис. 3.5) ММ1 = dS. Работу силы F на перемещение dS можно вычислить как сумму работ ее составляющих Fx, Fy, Fz на перемещения dx, dy, dz.
Рис. 3.5
Работа силы на любом конечном перемещении М0М1 (см. рис. 3.4) вычисляется как интегральная сумма соответствующих элементарных работ или Если Такой случай имеет место; когда действующая сила постоянна по модулю и направлению ( Единицы измерения: в системе СИ – джоуль (1 Дж = 1 Н·м); в системе СГС – 1 кг·м. Мощностью называется величина, определяющая работу, соверша-емую силой в единицу времени. Если работа совершается равномерно, то мощность где t1 – время, в течение которого произведена работа.
Рис. 3.6
В общем случае где V – скорость движения. Единицы измерения: в системе СИ – ватт (1 Вт = 1 в системе СГС – В технике часто используется лошадиная сила (л. с.): 1 л. с. = 75
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 368. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
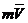 , равная произведению массы точки на вектор ее скорости
, равная произведению массы точки на вектор ее скорости 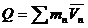 . Направлен вектор
. Направлен вектор 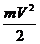 .
.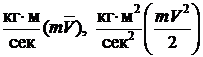 ;
;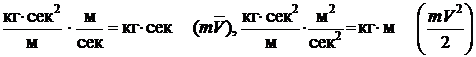 .
.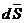 , равная произведению вектора силы
, равная произведению вектора силы 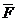 на элементарный промежуток времени
на элементарный промежуток времени 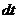 :
: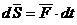 . (3.13)
. (3.13) 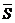 любой силы
любой силы 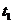 вычисляется как интегральная сумма
вычисляется как интегральная сумма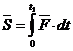 . (3.14)
. (3.14)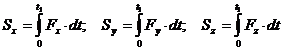 . (3.15)
. (3.15)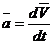 , то урав-
, то урав-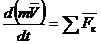 . (3.16)
. (3.16)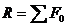 , имеет в момент времени t = 0 скорость V0, а в момент t1 – скорость V1
, имеет в момент времени t = 0 скорость V0, а в момент t1 – скорость V1 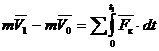 .
.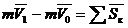 . (3.17)
. (3.17)
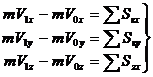 (3.18)
(3.18)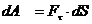 , (3.19)
, (3.19) – проекция силы на касательную к траектории;
– проекция силы на касательную к траектории;
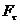 и Fn, то изменять скорость точки будет составляющая
и Fn, то изменять скорость точки будет составляющая 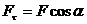 , получаем из равенства (3.19)
, получаем из равенства (3.19)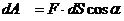 (3.20)
(3.20) острый, то работа положительная;
острый, то работа положительная; – работа равна нулю.
– работа равна нулю.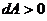 , то сила ускоряет движение;
, то сила ускоряет движение;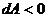 , то сила замедляет движение.
, то сила замедляет движение.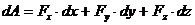 . (3.21)
. (3.21)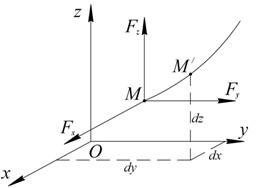
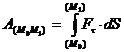 (3.22)
(3.22)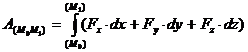 (3.23)
(3.23)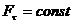 , то
, то 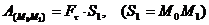 .
.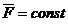 ) (рис. 3.6).
) (рис. 3.6).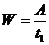 , (3.24)
, (3.24)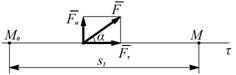
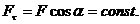
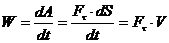 , (3.25)
, (3.25)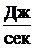 );
);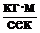 .
.