
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свободные колебания без учёта сил сопротивленияРассмотрим точку М, движущуюся под действием одной только восстанавливающей силы F, направленной к неподвижному центру и пропорциональной расстоянию от этого центру (рис. 3.8).
Рис. 3.8
Проекция силы Найдём закон движения точки С, составим дифференциальные уравнения движения Разделив обе части на m и введя обозначение
приведём уравнение к виду
Уравнение (3.31) представляет собой дифференциальное уравнение свободных колебаний при отсутствии сопротивления. Решение этого однородного дифференциального уравнения ищут в виде Полагая в уравнении (3.31) Общее решение уравнения (3.31)
Если вместо постоянных
или
Скорость точки в рассматриваемом движении
Колебания, совершаемые точкой по закону (3.32), называются гармоническими колебаниями. График их при
Рис. 3.9
Рассмотрим точку B, равномерно на окружности из скольжения Пусть постоянная угловая скорость вращения радиусов равна 
Рис. 3.10
Величина а называется амплитудой колебаний (она определяет их начальную фазу), Промежуток времени Т, в течение которого точка совершает одно полное колебание, называется периодом колебаний. По истечении этого периода фаза изменяется на
Величина Отметим, что свободные колебания при отсутствии сопротивления обладают следующими свойствами: 1. Амплитуда и начальная фаза колебаний зависят от начальных условий. 2. Частота k, а следовательно, и период Т от начальных условий Рассмотрим влияние постояннойсилы на свободные колебания точки (рис. 3.11). Пусть на точку М кроме восстанавливающей силы F действует постоянная по модулю и направлению сила Р. Величина силы F по-прежнему пропорциональна расстоянию от центра О, т. е. Очевидно, что в этом случае положением точки М будет центр
или где
Рис. 3.11
Примем
и, учитывая, что
что полностью совпадает с уравнением (3.31). Постоянная сила Р не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы F, а только смещает центр этих колебаний в сторону действия силы Р на величину статического отклонения
Из (3.36) имеем:
Тогда из равенства (3.35) следует, что
В частности, если Р – сила тяжести,
Свободные колебания при сопротивлении, |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 428. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

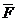 на ось Ox будет равна
на ось Ox будет равна  . Сила
. Сила  .
.
 (3.30)
(3.30) ,
, 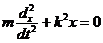 . (3.31)
. (3.31) .
. .
. . (3.32)
. (3.32) и
и 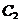 ввести постоянные
ввести постоянные 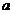 и
и 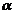 , такие, что
, такие, что  ,
,  , то получим:
, то получим:
 . (3.33)
. (3.33) . (3.34)
. (3.34) представлен
представлен 
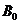 , определяется углом ДОВ0 = α (рис. 3.10).
, определяется углом ДОВ0 = α (рис. 3.10). . Тогда в произвольный момент t угол
. Тогда в произвольный момент t угол 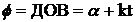 и легко увидеть, что проекция М точки В на диаметр движется по закону
и легко увидеть, что проекция М точки В на диаметр движется по закону 
 – фазой,
– фазой,  круговой частотой колебаний.
круговой частотой колебаний. . Следовательно,
. Следовательно,  , откуда
, откуда . (3.35)
. (3.35) – частота колебаний.
– частота колебаний. .
. , отстраненный от оси О на расстояние
, отстраненный от оси О на расстояние  , которое определяется равенством
, которое определяется равенством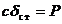
 , (3.36)
, (3.36) –статическое отклонение точки.
–статическое отклонение точки.

 ,
,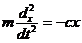 или
или  .
.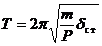 . (3.37)
. (3.37) , то формула (3.37) имеет вид
, то формула (3.37) имеет вид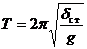 . (3.37/)
. (3.37/)