
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема об изменении кинетической энергии точкиРассмотрим точку массой m, перемещающуюся под действием приложенных к ней сил из положения М0, где она имела скорость V0, в положение М1, где ее скорость V1. Основной закон динамики Проектируем обе части равенства на касательную Ускорение представим в виде В результате имеем: Умножим обе части этого равенства на dS, внесем m под знак дифференциала. Тогда, замечая, что Проинтегрировав обе части этого равенства в пределах соответствующих значений переменных в точках М0 и М1 получим: Уравнение (3.27) выражает теорему об изменении кинетической энергии в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении. Теорема об изменении момента количества движения (теорема моментов) Иногда при изучении движения точки вместо изменения самого вектора m Момент вектора m  По модулю
Рис. 3.7
Теорема моментов относительно оси Рассмотрим материальную точку массы m, движущуюся под действием силы По полученным ранее формулам (статика) Аналогично и для момента
Беря от обеих частей этого равенства производные по времени, находим:
В правой части выражение в первых скобках равно 0, так как
Выражение во вторых скобках согласно формуле (*) равно
Окончательно имеем: Полученное уравнение выражает теорему моментов относительно оси: производная по времени от момента количества движения точки относительно какой-нибудь оси равна моменту действующей силы относительно той же оси. Из уравнения (3.28) следует, если Теорема моментов относительно центра Ранее было показано, что
Аналогично
При этом вектор Дифференцируем выражение
но
или Теорема моментов. Производная по времени от момента количества движения точки, взятого относительно какого-либо неподвижного центра, равна моменту действующей на точку силы относительно того же центра.
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 360. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
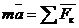 .
. к траектории точки М, направленную в сторону движения; получим:
к траектории точки М, направленную в сторону движения; получим: .
. .
. .
. , где
, где  – элементарная работа
– элементарная работа  , получаем выражение теоремы об изменении кинетической энергии в дифференциальной форме:
, получаем выражение теоремы об изменении кинетической энергии в дифференциальной форме: . (3.26)
. (3.26) . (3.27)
. (3.27) 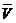 оказывается необходимым рассматривать изменение его момента.
оказывается необходимым рассматривать изменение его момента. и
и  и называется моментом количества движения, или кинетическим моментом точки относительно этого центра (оси). Вычисляется момент вектора m
и называется моментом количества движения, или кинетическим моментом точки относительно этого центра (оси). Вычисляется момент вектора m  , где h – длина перпендикуляра, опущенного из центра О на направление вектора m
, где h – длина перпендикуляра, опущенного из центра О на направление вектора m 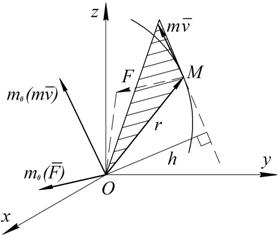
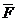 . Найдем для нее зависимость между моментами векторов m
. Найдем для нее зависимость между моментами векторов m  . (*)
. (*) , если вынести m за скобку,
, если вынести m за скобку, .
. .
. .
. , так как по основному закону динамики
, так как по основному закону динамики .
. . (3.28)
. (3.28) , то
, то 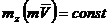 .
. .
. .
. направлен перпендикулярно плоскости, проходящей через центр О и вектор
направлен перпендикулярно плоскости, проходящей через центр О и вектор  , а вектор
, а вектор  перпендикулярен плоскости, проходящей через центр О и вектор
перпендикулярен плоскости, проходящей через центр О и вектор 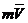 .
.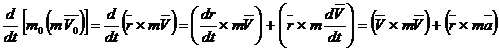 ,
, как вектор производной двух параллельных векторов,
как вектор производной двух параллельных векторов,  . Следовательно,
. Следовательно,
 (3.29)
(3.29)