
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вынужденные колебания. РезонансРассмотрим случай колебаний, когда на точку, кроме восстанавливающей силы F, действует ещё периодически изменяющаяся со временем сила
Эта сила называется возмущающей; колебания, происходящие под ее действием, – вынужденными. Величина p называется частотой возмуща-ющей силы. Возмущающая сила может изменяться и по другому закону. Мы ограничимся, когда возмущающая сила изменяется по гармоническому закону. Вынужденные колебания при отсутствии сопротивления Дифференциальное уравнение движения имеет вид
Разделим обе части на m, полагая, что
Тогда, учитывая обозначения (3.30), приведем уравнение движения
Выражение (3.45) является дифференциальным уравнением вынужденных колебаний точки, при отсутствии сопротивления. Если решение состоит из общего и частного, то
Полагая, что
где А – постоянная величина, которую надо подобрать так, чтобы уравнение (3.45) обратилось в тождество. Подставив
Таким образом, частным решением будет выражение
Общее решение уравнения (3.45) имеет вид
где a и Решение (3.47) показывает, что колебания точки складываются из собственных (с амплитудой а, зависящей от начальных условий, и частотой k) и вынужденных (с амплитудой А и частотой р)колебаний. Благодаря наличию тех или иных сопротивлений собственные колебания будут довольно быстро затухать, поэтому основным значением в рассматриваемом движении имеют вынужденные колебания, закон которых даётся уравнением (3.46).  Частота р вынужденных колебаний равна частоте возмущающей силы. Амплитуду этих колебаний, если разделить числитель и знаменатель на
где согласно уравнениям (3.30) и (3.44)
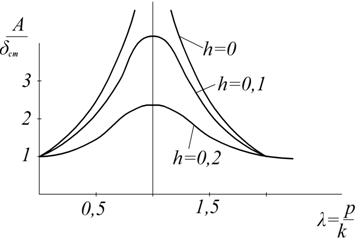
Рис. 3.14 (h = 0)
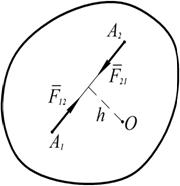
При р = 0 (или р = k амплитуда А становится очень большой; В случае, когда р = k, т. е. частота возмущённой силы равна частоте собственных колебаний, имеет место так называемое явление резонанса. РАЗДЕЛ IV. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА ВВЕДЕНИЕ В ДИНАМИКУ СИСТЕМЫ Механическая система Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки зависит от положения и движения всех остальных. Материальное тело будем рассматривать как систему материальных точек, образующих это тело. Примером может служить любая машина или механизм, в которой Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих самолетов), механическую систему Внешними называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы. Внутренними являются силы, действующие на точки системы со стороны других точек или тел этой же системы. Внутренние силы обладают следующими свойствами: 1. Геометрическая сумма (главный вектор) всех внутренних сил системы равна нулю. По третьему закону динамики любые две точки системы действуют друг на друга с равными по модулю и противоположно направленными силами. Так как аналогичный результат имеет место для любой пары точек системы (рис. 4.1), то
Рис. 4.1
2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равна нулю. Возьмем произвольный центр О. Как видно из рис. 4.1,
Масса системы. Центр масс Движение системы, кроме действующих сил, зависит от ее суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образовавших систему:
В однородном поле тяжести, для которого
где mк – массы материальных точек; хк, yк, zк – координаты этих точек. Геометрическая точка С, координаты которой определяются формулами (4.1), называется центром масс. Если положение центра масс определять его радиусом-вектором где В однородном поле тяжести положение центра масс и центра тяжести совпадает. Понятие о центре тяжести как о точке, через которую проходит линия действия равнодействующих сил тяжести, имеет значение только для твердого тела, находящегося в однородном поле тяжести. Понятие же о центре масс как о характере распределения масс в системе материальных точек или тел, имеет смысл для любой системы материальных точек или тел.
|
||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 380. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
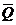 , проекция
, проекция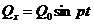 . (3.43)
. (3.43)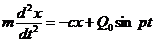 .
.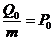 . (3.44)
. (3.44)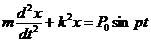 . (3.45)
. (3.45)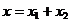 .
.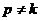 , частные решения
, частные решения 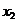 находим как
находим как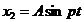 ,
,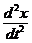 в формулу (3.45), имеем:
в формулу (3.45), имеем:
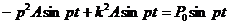
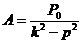 .
.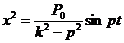 . (3.46)
. (3.46)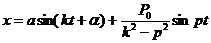 , (3.47)
, (3.47)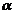 – постоянные интегрирования.
– постоянные интегрирования.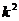 , можно представить в виде
, можно представить в виде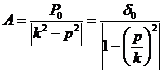 , (3.48)
, (3.48)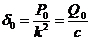 , т. е.
, т. е. 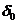 – величина статического отклонения точки под действием силы
– величина статического отклонения точки под действием силы 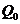 . Как видим,
. Как видим,  (рис. 3.14).
(рис. 3.14).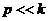 ) амплитуда А равна (3.48);
) амплитуда А равна (3.48);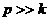 – очень малой.
– очень малой.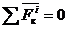 .
.
 . Аналогичный результат получится при вычислении моментов относительно оси
. Аналогичный результат получится при вычислении моментов относительно оси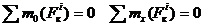 .
.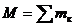 .
.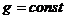 , вес любой частицы тела будет пропорционален ее массе, поэтому о распределении масс в теле можно судить по положению его центра тяжести.
, вес любой частицы тела будет пропорционален ее массе, поэтому о распределении масс в теле можно судить по положению его центра тяжести.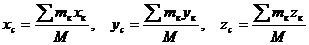 , (4.1)
, (4.1) , то из равенств (4.1) следует:
, то из равенств (4.1) следует: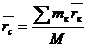 , (4.1/)
, (4.1/) – радиусы-векторы точек, образовавших систему.
– радиусы-векторы точек, образовавших систему.