
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сложение поступательных движенийПусть твердое тело движется поступательно со скоростью
Рис. 2.39
Так как относительное движение – поступательное, то относительные скорости всех точек тела геометрически равны Переносное движение также поступательное, т. е. переносные скорости всех точек тела геометрически равны Следовательно, по теореме сложения скоростей, все точки тела в абсолютном движении будут иметь одну и ту же скорость Итак, при сложении двух поступательных движений со скоростями Задача сложения скоростей в этом случае сводится к задаче кинематической точки.
Сложение вращений вокруг двух параллельных осей Рассмотрим случай, когда относительное движение тела является вращением с угловой скоростью Исследуем отдельно случаи, когда вращения направлены в одну или разные стороны.
Рис. 2.40 Вращения, направленные в одну сторону  Изобразим сечение (S) тела плоскостью, перпендикулярной осям Следы осей в сечении (S) изображены буквами А и В. Легко видеть, что точка А, как лежащая на оси Аа/, получает скорость только от вращения вокруг оси Вb/, следовательно
Рис. 2.41
Для определения угловой скорости
Из свойств пропорций
Подставляя
Итак, если тело участвует одновременно в двух направленных С течением времени мгновенная ось вращения Сс/ будет менять свое положение, описывая цилиндрическую поверхность.
Вращения, направленные в разные стороны Допустим для определения Рассуждая, как и в предыдущем случае, получим:
Рис. 2.42
При этом векторы
или по свойствам пропорций
Подставляя значения
Итак, в этом случае результирующее движение также является мгновенным вращением с абсолютной угловой скоростью Пара вращений Рассмотрим частный случай, когда вращения вокруг параллельных осей направлены в разные стороны, но по модулю
т. е.
находиться в бесконечности и все точки тела в данный момент будут иметь одинаковые скорости Следовательно, результирующее движение тела будет поступательным (или мгновенно-поступательным) движением со скоростью Иначе говоря, пара вращений эквивалентна поступательному (или мгновеннопоступа-
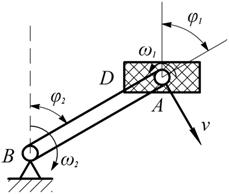
моменту пары угловых скоростей этих вращений. Примером такого движения является поступательное движение велосипедной педали DE относительно рамы велосипеда, являющееся результатом относительного вращения педали вокруг оси А, укрепленной на кривошипе ВА и переносного вращения кривошипа ВА вокруг оси В (рис. 2.44). Угловые скорости
6.4.Сложение вращений вокруг пересекающихся осей Рассмотрим случай сложения вращения вокруг двух пересекающихся осей (рис. 2.45). Когда абсолютное движение тела является результатом относительного и переносного вращений с угловыми скоростями
Чтобы определить вектор скорость какой-нибудь точки М тела, ра- Рис. 2.45 диус-вектор которой
В относительном движении вокруг оси Оа точка М получает скорость Следовательно, абсолютная скорость точки М
С другой стороны, так как результирующее движение тела является мгновенным вращением с некоторой угловой скоростью Такие результаты будут получаться для всех точек тела (т. е. при любых Следовательно, при сложном вращении вокруг двух осей, пересекающихся в точке О, результирующее движение будет мгновенным вращением вокруг оси Ос, проходящей через эту точку, причем угловая скорость С течением времени ось Ос меняет свое положение, описывая коническую поверхность, вершина которой находится в точке О. Если тело участвует одновременно в мгновенных вращениях вокруг нескольких осей, пересекающихся в точке О, то, применяя полученное равенство (
|
||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 403. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 относительно системы отсчета 0хуz, которая в свою очередь, движется поступательно со скоростью
относительно системы отсчета 0хуz, которая в свою очередь, движется поступательно со скоростью  по отношению к неподвижной системе отсчета 0х1у1 (рис. 2.39).
по отношению к неподвижной системе отсчета 0х1у1 (рис. 2.39).
 , т. е. абсолютное движение тела будет поступательным.
, т. е. абсолютное движение тела будет поступательным. вокруг оси
вокруг оси  , укрепленный на кривошипе ba вокруг оси
, укрепленный на кривошипе ba вокруг оси  с угловой скоростью
с угловой скоростью  (рис. 2.40). Если
(рис. 2.40). Если  параллельны, то движение тела будет плоскопараллельным по отношению к плоскости, перпендикулярной осям.
параллельны, то движение тела будет плоскопараллельным по отношению к плоскости, перпендикулярной осям.
 . Точно также
. Точно также  . При этом векторы
. При этом векторы  и
и 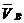 параллельны друг другу (оба перпендикулярны АВ) и направлены в разные стороны. Тогда точка С является МЦС (
параллельны друг другу (оба перпендикулярны АВ) и направлены в разные стороны. Тогда точка С является МЦС (  ), а следовательно, ось Сс/ параллельна осям Аа/ и Вв/ является мгновенной осью вращения тела.
), а следовательно, ось Сс/ параллельна осям Аа/ и Вв/ является мгновенной осью вращения тела.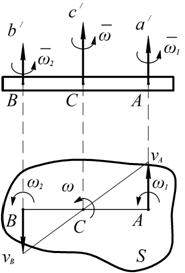
 абсолютного вращения тела вокруг оси Сс/ и положения самой оси, т. е. точки С, воспользуемся равенством
абсолютного вращения тела вокруг оси Сс/ и положения самой оси, т. е. точки С, воспользуемся равенством .
.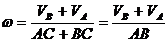
 (2.33)
(2.33) .
. (рис. 2.42).
(рис. 2.42). 
 параллельны и направлены в одну сторону. Тогда мгновенная ось вращения проходит через точку С, причем
параллельны и направлены в одну сторону. Тогда мгновенная ось вращения проходит через точку С, причем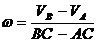 .
. и
и  , получим:
, получим: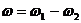 , (2.34)
, (2.34) .
. (рис. 2.43). Такая совокупность вращения называется парой вращений, а векторы
(рис. 2.43). Такая совокупность вращения называется парой вращений, а векторы  и
и  образуют пару угловых ускорений:
образуют пару угловых ускорений: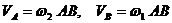 ,
, .
. Тогда мгновенный центр скоростей будет
Тогда мгновенный центр скоростей будет .
. , численно равной
, численно равной  и направленной перпендикулярно плоскости, проходящей через векторы
и направленной перпендикулярно плоскости, проходящей через векторы  . Скорость поступательного движения педали
. Скорость поступательного движения педали  .
.
 Следовательно, результирующее дви-жение тела является движением вокруг неподвижной точки О и для каждого элементарного промежутка времени представляет собой элементарный поворот с угловой скоростью
Следовательно, результирующее дви-жение тела является движением вокруг неподвижной точки О и для каждого элементарного промежутка времени представляет собой элементарный поворот с угловой скоростью 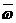 , вычислим
, вычислим .
. , в переносном же движении вокруг оси Оb она получает скорость
, в переносном же движении вокруг оси Оb она получает скорость  .
. .
. .
. ). Отсюда заключаем, что
). Отсюда заключаем, что . (2.35)
. (2.35)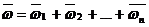 . (2.36)
. (2.36)