
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
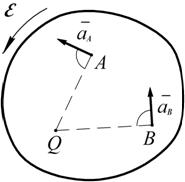
Мгновенный центр ускорений (МЦУ)Мгновенным центром ускорений (МЦУ)называется точка плоской фигуры, ускорение которой равно нулю. Если в данный момент времени задано ускорение Проведем из точки А полупрямую АN под углом
Рис. 2.33 На полупрямой отложим отрезок Полученная точка Ускорение точек плоской фигуры как ускорение во вращательном движении вокруг МЦУ Примем точку Имеем:
Таким образом, ускорение любой точки плоской фигуры можно определить как ускорение этой точки при вращении вокруг неподвижной оси, проходящей через МЦУ. Частные случаи определения МЦУ 1. Известна точка, ускорение которой равно нулю. Эта точка и является МЦУ. Например, качение без скольжения колеса по прямолинейному рельсу с постоянной скоростью центра С (рис. 2.34). Так как Ускорение любой точки, например В,
так как
Рис. 2.34
2. Равномерное вращение: В этом случае
Следовательно, ускорения всех точек направлены к МЦУ (рис. 2.36), причем расстояние от точки до МЦУ определяется по формуле
Рис. 2.35
3. Момент, когда угловая скорость становится равной нулю:
В этом случае т. е. ускорения всех точек направлены перпендикулярно к отрезкам, соединяющим эти точки с МЦУ. Расстояние 
Рис. 2.36
4. Момент времени, когда угловая скорость и угловое ускорение становятся равными нулю при непоступательном движении твердого тела:
В этом случае ускорение любой точки равно ускорению полюса
Рис. 2.37
Основные способы вычисления углового ускорения при плоском движении 1. Если известен закон изменения угла поворота или угловой скорости от времени, то угловое ускорение 2. 3. Когда расстояние от точки, ускорение которой известно, до МЦС остается постоянным во время движения плоской фигуры, угловое ускорение рассчитывается следующим способом. Рассмотрим качение без скольжения колеса по неподвижной прямой линии (рис. 2.38).
Дифференцируем
Так как в данном случае центр колеса движется Рис. 2.38 прямолинейно, то
СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 590. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 какой-то
какой-то 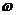 и
и 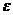 известны, то положение МЦУ определяется следующим образом.
известны, то положение МЦУ определяется следующим образом. к ускорению
к ускорению 
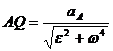 .
. и есть МЦУ.
и есть МЦУ. .
. , то
, то 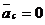 , т. е. точка С и есть МЦУ.
, т. е. точка С и есть МЦУ.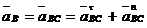 ;
; ,
, .
. Таким образом,
Таким образом, 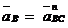 , т. е. ускорение каждой точки колеса направлено к МЦУ.
, т. е. ускорение каждой точки колеса направлено к МЦУ. .
. .
.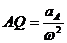 .
.
 .
. .
.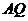 вычисляется по формуле
вычисляется по формуле 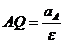 .
.
 .
.
 определяется путем дифференцирования:
определяется путем дифференцирования: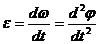 .
. Угловая скорость
Угловая скорость  .
. ):
): .
. .
.