
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Мгновенный центр скоростей (МЦС)МЦС называется точка плоской фигуры, скорость которой в данный момент времени равна нулю. Теорема. Если угловая скорость плоской фигуры не равна нулю, то МЦС существует. Доказательство. Пусть скорость точки А не равна нулю, Вычислим скорость точки Р, отстоящей от точки А на расстоянии Тогда Так как Вектор Рис. 2.24
Определение скорости точки плоской фигуры с помощью МЦС Выберем за полюс точку Р (рис. 2.25). Тогда скорость произвольной точки А
Таким образом, скорости точек тела при его плоском движении распределяются так же, как при вращательном движении тела вокруг неподвижной оси. Роль неподвижной оси играет мгновенная ось, проходящая через МЦС перпендикулярно плоской фигуре. Следовательно, скорости всех точек плоской фигуры перпендикулярны отрезкам, соединяющим эти точки с МЦС, а модули скоростей пропорциональны расстояниям от точек до МЦС.
Рис. 2.25 ) Определение угловой скорости плоской фигуры Угловая скорость плоской фигуры определяется одним единственным способом: она равна скорости любой точки плоской фигуры, деленной на расстояние от этой точки до МЦС: Частные случаи определения положения МЦС 1. МЦС находится в точке пересечения перпендикуляров с векторами скоростей двух точек плоской фигуры (рис. 2.26).
Рис. 2.26 
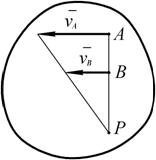
2. Соединяем концы векторов. МЦС находится на пересечении линии, соединяющей концы векторов с линией АВ (рис. 2.27).
Рис. 2.27
3.
Рис. 2.28
4.
Тогда скорости определяются как
В данный момент времени скорости всех точек плоской фигуры геометрически равны. Имеем мгновенно поступательное распределение скорости, при этом угловая скорость равна нулю, а МЦС находится в Рис. 2.29 бесконечности.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 415. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 > 0
> 0 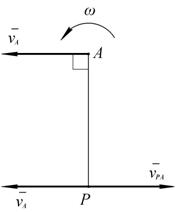 АР =
АР =  , причем
, причем  .
. .
. , то
, то  , причем
, причем  .
. направлен противоположно
направлен противоположно  , т. е. можно записать:
, т. е. можно записать:  ,
,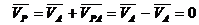 .
. , так как
, так как 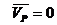 .
. (2.28
(2.28
 (2.29)
(2.29)

 , так как точки касания обоих тел при отсутствии скольжения должны иметь одинаковую скорость, а второе тело неподвижно (рис. 2.28).
, так как точки касания обоих тел при отсутствии скольжения должны иметь одинаковую скорость, а второе тело неподвижно (рис. 2.28).
 , но
, но  не перпендикулярен
не перпендикулярен  (рис. 2.29).
(рис. 2.29).
 .
. .
.