
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сложение ускорений. Теорема КориолисаНайдем зависимость между абсолютным При определении
Рис. 2.16
Условимся обозначать элементарное перемещение, получаемое вектором при абсолютном перемещении, символом d, относительном – d1 и переносном – d2. Тогда где Поскольку при сложном движении
Однако в этом равенстве, Для получения искомых зависимостей учтем, что абсолютное перемещение где  Отношение При поступательном перемещении вектор Следовательно,
где В результате из равенства (**) находим: По аналогии с (**) величину где Согласно (*) Скорость точки в случае плоскопоступательного движения ( Когда переносное движение не является поступательным ( Чтобы найти Тогда будем иметь:
Следовательно,
В результате из равенства (***) находим: Найденные в ходе расчетов соотношения (А, В) показывают, что в общем случае производные Введем обозначение Величина Окончательно получим: Формула выражает теорему Кориолиса: абсолютное ускорение точки равно геометрической сумме трех ускорений: относительного, характеризующего изменение относительной скорости точки в относительном движении, переносного, определяющего изменение переносной скорости точки в переносном движении, и кориолисова, характеризующего изменение относительной скорости в переносном движении и переносной скорости в относительном движении. Если переносное движение поступательное, то Направление Чтобы определить направление вектора ускорения Кориолиса, необходимо вектор относительной скорости спроектировать на плоскость, перпендикулярную вектору угловой скорости переносного вращения; полученный при этом вектор следует повернуть в этой плоскости на
Рис. 2.17
Причины появления ускорения Кориолиса Причиной появления ускорения Кориолиса является взаимное влияние относительного движения на переносное и переносного на относительное, в результате чего переносная скорость меняет модуль и направление, а вектор относительной скорости – направление. Пример. Пусть по радиусу диска, вращающегося вокруг оси, перпендикулярной его плоскости , перемещается равномерно человек с относительной скоростью Пусть в момент времени
Рис. 2.18
Очевидно, что за время
В результате относительного движения человека из точки М в точку М/ модуль переносной скорости изменяется:
Указанные изменения и вызывают появление кориолисова ускорения.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 416. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , относительным
, относительным  и переносным
и переносным  ускорениями. Эти величины отличаются не только тем, что при их вычислении рассматриваются приращения разных векторов скоростей, но и тем, что эти приращения рассчитываются на разных перемещениях (рис. 2.16).
ускорениями. Эти величины отличаются не только тем, что при их вычислении рассматриваются приращения разных векторов скоростей, но и тем, что эти приращения рассчитываются на разных перемещениях (рис. 2.16).
 , при вычислении
, при вычислении  на относительном элементарном перемеще-
на относительном элементарном перемеще-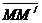 и при вычислении
и при вычислении  на переносном элементарном перемещении
на переносном элементарном перемещении  .
.
 (*)
(*) – элементарное приращение вектора
– элементарное приращение вектора  – элементарное приращение вектора
– элементарное приращение вектора  – элементарное приращение вектора
– элементарное приращение вектора 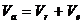 , то
, то
 ,
,  , как и
, как и 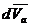 , представляют собой элементарные приращения векторов на абсолютном перемещении
, представляют собой элементарные приращения векторов на абсолютном перемещении 
 и
и 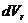 (элементарное приращение вектора
(элементарное приращение вектора  , (**)
, (**) – элементарное приращение, получаемое тем же вектором на переносном перемещении
– элементарное приращение, получаемое тем же вектором на переносном перемещении 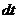 и дает согласно (*) величину
и дает согласно (*) величину 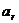 . Для вычисления
. Для вычисления  .
.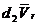 на перемещении
на перемещении 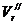 и А// В// изображают вектор
и А// В// изображают вектор  , а пунктиром показан вектор
, а пунктиром показан вектор 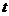 ). Приращение, получаемое вектором при таком повороте, определяется формулой
). Приращение, получаемое вектором при таком повороте, определяется формулой  .
. и
и  ,
,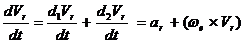 (А)
(А) (элементарное приращение вектора
(элементарное приращение вектора  , (***)
, (***) – элементарное приращение, получаемое вектором
– элементарное приращение, получаемое вектором  .
.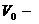 скорость полюса)
скорость полюса) . (****)
. (****) ), значения
), значения  в точках М и М/ будут разными. Вследствие этого вектор
в точках М и М/ будут разными. Вследствие этого вектор  – значение
– значение  и
и  изменяется только в относительном движении.
изменяется только в относительном движении. , где
, где  .
. .
. . (В)
. (В) действительно отличаются от
действительно отличаются от  , причем на одну и ту же величину (
, причем на одну и ту же величину ( 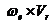 ).
). . (2.25)
. (2.25) , характеризующая изменения вектора относительной скорости
, характеризующая изменения вектора относительной скорости  в переносном движении и вектора
в переносном движении и вектора  . (2.26)
. (2.26) и
и  . Тогда
. Тогда 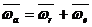 .
. определяется по правилу векторного произведения, а также по правилу Н.Е. Жуковского.
определяется по правилу векторного произведения, а также по правилу Н.Е. Жуковского.
 , т. е. переносная скорость человека – скорость той точки диска, где в данный момент времени находится человек.
, т. е. переносная скорость человека – скорость той точки диска, где в данный момент времени находится человек.
 относительная скорость изменяется по направлению от
относительная скорость изменяется по направлению от  вследствие вращательного переносного движения.
вследствие вращательного переносного движения. .
.