
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Скорость и ускорение точки твердого тела, вращающегося вокруг неподвижной оси
При вращении точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна к оси вращения, а центр С лежит на самой оси. Если за время Рис. 2.10
Скорость Как следует из формулы, линейные скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения (рис. 2.11).
Рис. 2.11 Для нахождения ускорения точки М воспользуемся формулами:
В нашем случае
или окончательно
Касательное ускорение 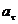 направлено по касательной к траектории направлено по касательной к траектории (в сторону движения, если тело вращается ускоренно, или в обратную, если тело вращается замедленно); нормальное  всегда направлено по радиусу h к оси вращения (рис. 2.12). всегда направлено по радиусу h к оси вращения (рис. 2.12).
Рис. 2.12
Полное ускорение точки М
или Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом
Подставляя значения
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ Основные понятия Сложным движением называется движение точки относительно двух систем отсчета, одна из которых неподвижна, а другая произвольно перемещается относительно неподвижной системы координат. 
Движение точки М отно-сительно подвижной системы координат (О, х, у, z), называется относительным, а скорость и Рис. 2.13 ускорение в этом движении –
относительной скоростью и относительным ускорением и обозначаются Подвижная система координат и все, что с ней неразрывно связано, называется переносной средой. Движение точки М вместе с подвижной системой координат относительно неподвижной называется переносным движением. Скорость (ускорение) той точки переносной среды, с которой в данный момент времени совпадает наша точка, называется переносной скоростью (ускорением), обозначается Примером может служить движение человека по эскалатору: движение эскалатора является переносным, перемещение человека вниз или вверх по эскалатору – относительным, а движение по отношению к неподвижным стенам – абсолютное. Движение точки М по отношению к неподвижной системе отсчета, которое названо абсолютным, является сложным, состоящим из относительного и переносного движения точки. Основная задача изучения сложного движения состоит в установлении зависимостей между скоростями и ускорениями относительного, переносного и абсолютного движения точки. Сложение скоростей Рассмотрим точку М, совершающую сложное движение. Пусть эта точка, двигаясь вдоль своей относительной траектории АВ, совершает за промежуток времени
Рис. 2.14 Сама кривая АВ, двигаясь вместе с подвижными осями (О, х, y, z) Одновременно та же точка кривой АВ, с которой в момент времени Из векторного треугольника ММ//М1 Деля обе части на По определению Что касается последнего соотношения, то, так как при В результате находим: Таким образом, мы доказали теорему о сложении скоростей: при сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей. Пусть векторы направлены по касательным к соответствующим траекториям (рис. 2.15).
Рис. 2.15
Модуль абсолютной скорости:
С помощью параллелограмма скоростей решается ряд задач кинематики точки: 1) имея значения 2) зная 3) если известны скорость
|
|||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 444. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Рассмотрим точку М, находящуюся на расстоянии h от оси
Рассмотрим точку М, находящуюся на расстоянии h от оси  происходит элементарный поворот тела на угол
происходит элементарный поворот тела на угол 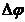 , то точка М при этом совершит вдоль своей траектории элементарное перемещение
, то точка М при этом совершит вдоль своей траектории элементарное перемещение  . Тогда скорость точки будет
. Тогда скорость точки будет или
или  (2.22)
(2.22) называют еще линейной, или окружной, скоростью
называют еще линейной, или окружной, скоростью 
 .
. . Подставляя значение
. Подставляя значение 



 (2.23)
(2.23) , который вычисляется по формуле
, который вычисляется по формуле
 и
и 
 Движение точки М относи-тельно неподвижной системы координат (О, х1, у1, z1) называется абсолютным (рис. 2.13), а скорость и ускорение в этом движении – абсолютной скоростью и абсолютным ускорением и обозначаются
Движение точки М относи-тельно неподвижной системы координат (О, х1, у1, z1) называется абсолютным (рис. 2.13), а скорость и ускорение в этом движении – абсолютной скоростью и абсолютным ускорением и обозначаются 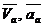 .
. .
. .
. относительное перемещение, определяемое вектором
относительное перемещение, определяемое вектором 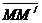 (рис. 2.14).
(рис. 2.14).
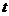 совпадает точка М, совершит переносное перемещение,
совпадает точка М, совершит переносное перемещение,  . В результате точка М придет в положение М1 и совершит за время
. В результате точка М придет в положение М1 и совершит за время  абсолютное перемещение
абсолютное перемещение  .
.

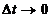
 .
.  .
.  . (2.24)
. (2.24)

 и
и  , можно найти абсолютную скорость;
, можно найти абсолютную скорость; и направления скоростей
и направления скоростей  , можно найти модули этих скоростей,
, можно найти модули этих скоростей, .
.