
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вращательное движение твердого телаВращательным называется такое движение твердого тела, при котором точки тела движутся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения тела, и описывает окружности, центры которых лежат на этой оси. На рис. 2.9 АВ – ось вращения, Р – неподвижная плоскость, Q – подвижная плоскость. Двухгранный угол Угол поворота будем считать положительным, если можно смотреть навстречу оси вращения и видеть его направление против часовой стрелки. Численное значение угла поворота выражается в радианах: Угол поворота (в радианах) часто выражают через число оборотов N:
Угол его можно рассматривать как угловую координату тела: Выражение (2.18) является уравнением вращательного движения твердого тела. Главными кинематическими характеристиками вращательного движения твердого тела в целом являются угловая скорость Пусть в момент времени Предел отношения приращения угла к приращению времени при стремлении последнего к нулю, называется угловой скоростью тела в данный момент времени:
Размерность [ В технике часто при равномерном вращении используется числом оборотов в минуту Зависимость между 
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением: Весьма полезным является введение в рассмотрении вектора угловой скорости и вектора углового ускорения. Вектором угловой скорости будем называть вектор, модуль которого равен абсолютному значению производной угла поворота тела по времени, направленной вдоль оси вращения в ту сторону, откуда вращение тела видно происходит против часовой стрелки.
где Вектором углового ускорения будем называть вектор, равный производной по времени от вектора угловой скорости:
Вектор Уравнения равномерного вращения тела Вращение тела с постоянной угловой скоростью называется равномерным:
Проинтегрируем:
Уравнения равнопеременного вращения тела Вращение тела, при котором угловое ускорение постоянно, называется равнопеременным вращением. Если величина
Разделим переменные:
Проинтегрируем:
Разделим переменные:
Проинтегрируем:
В результате получим:
В общем случае
Знак «+» соответствует ускоренному вращению, «–» – замедленному.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 360. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
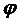 – угол поворота тела.
– угол поворота тела.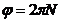 .
.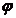 , определяет положение не только подвижной
, определяет положение не только подвижной 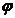 =
= 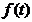 (2.19)
(2.19)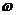 и угловое ускорение
и угловое ускорение 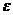 .
.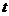 движение подвижной полуоси определяется углом
движение подвижной полуоси определяется углом 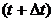 – углом
– углом 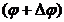 .
.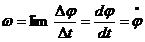 (2.20)
(2.20)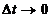
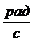 .
.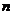 .
.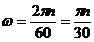 .
.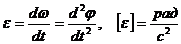 . (2.21)
. (2.21)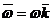 ,
,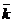 – единичный орт оси z.
– единичный орт оси z.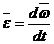 .
.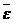 , как и вектор
, как и вектор 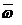 , направлен вдоль оси вращения твердого тела.
, направлен вдоль оси вращения твердого тела.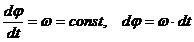 .
.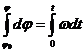 ,
,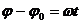 .
.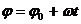 – уравнение равномерного вращения тела.
– уравнение равномерного вращения тела.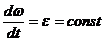
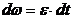 .
.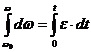 ,
,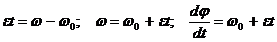 .
.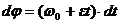 .
.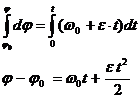
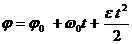
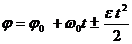 – уравнение равнопеременного движения.
– уравнение равнопеременного движения.