
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Главные векторы сил и моментовГлавным вектором системы сил называется геометрическая сумма сил системы.
Рассмотрим систему сил, как угодно ориентированных в пространстве (рис. 1.44); вычислим моменты этих сил относительно точки
Векторы
Рис. 1.44
Таким образом, главным моментом пространственной системы сил относительно центра называется геометрическая сумма моментов сил системы относительно того же центра. Главным моментом пространственной системы сил относительно неподвижной оси называется алгебраическая сумма моментов сил системы той же оси.
Приведение пространственной системы сил к заданному центру Приведение силы к заданному центру (метод Пуансо). Приведём силу к центру
Рис. 1.45
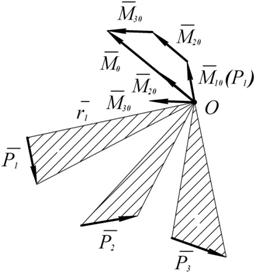
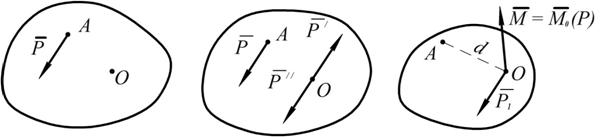
Силы При приведении сил к заданному центру получаем в этом центре силу, геометрически равную заданной, и пару сил, момент которой равен моменту силы относительно центра приведения. Теорема. При приведении пространственной системы сил к центру всегда получим силу, называемую главным вектором сил, приложенную в центре приведения, и пару, момент которой равен главному моменту системы сил относительно центра приведения. Доказательство: пусть имеем систему сил, как угодно ориентированных в пространстве (ограничимся тремя силами) (рис. 1.46). Каждую силу приводим к центру 
Рис. 1.46
Векторы моментов
Вычисление главного вектора и главного момента пространственной системы сил Главный вектор
Спроектируем обе части этого векторного соотношения на оси
Тогда модуль Направление
Рис. 1.47 Главный момент
Спроектируем данное векторное соотношение на оси x, y, z:
Модуль главного момента
Направление определяем направлением косинусов:
Условия и уравнения равновесия пространственной системы сил Теорема. Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент равнялись нулю. Доказательство. Достаточность. При Необходимость. Пусть данная система сил эквивалентна нулю. Тогда необходимо, чтобы Если какое-либо из этих условий не выполняется, то система сил приводится либо к Уравнения равновесия:
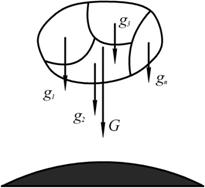
В случае произвольной пространственной системы сил задача является статически определенной, если число алгебраических неизвестных не более шести. ЦЕНТР ТЯЖЕСТИ Сила тяжести – равнодействующая сил притяжения к Земле, она распределена по всему объёму тела. Силы притяжения, приложенные к частицам твёрдого тела, образуют систему сил, линии действия которых сходятся в центре Земли. Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными (рис. 1.48).
Рис. 1.48
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей: Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси. Изображаем тело, составленное из нескольких частей, причем силы тяжести частей Пусть равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центре
Рис. 1.49 Из теоремы Вариньона следует:
В однородном теле сила тяжести пропорциональна объёму
где Следовательно, в формулах для однородных тел
где Центр тяжести однородных плоских тел (плоских фигур) Для плоских тел можно записать:
где Тогда после подстановки в записанные выше формулы получим:
где Выражение Аналогично Тогда координаты центра тяжести сечения можно выразить как
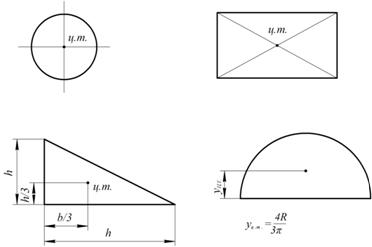
Оси, проходящие через центр тяжести, называются центральными. Статический момент относительно центральной оси равен нулю. Положение центра тяжести простых геометрических фигур представлено на рис. 1.50.
Рис. 1.50
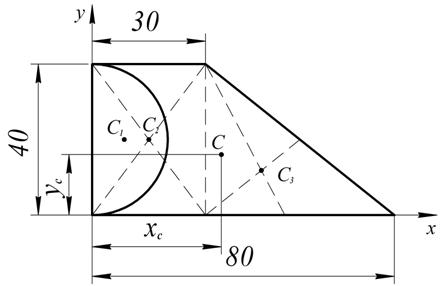
При решении задач необходимо учесть: 1. Центры тяжести симметричных фигур находятся на оси симметрии. 2. Сложные сечения разделяем на несколько простых. 3. Полости (отверстия) рассматриваются как часть сечения с отрицательной площадью. Пример. Необходимо определить центр тяжести представленного сечения (рис. 1.51).
Рис. 1.51
Разбиваем сечение на простейшие геометрические фигуры (прямоугольник, треугольник, половина круга). Площадь прямоугольника F1 = 40 30 = 1 200 см2. Площадь треугольника F2 = ½ ∙40 ∙50 = 1 000 см2. Площадь половины круга F3 = ∙(π 20)/2 = 628 см2. Центр тяжести: прямоугольника х1 = 15 см; y1 = 20 см; треугольника х2 = 30 + 1/350 = 46,7 см; y2 = 1/3 ∙ 40 = 13,3 см; половины круга х3 = 4R/3 π = 8,5 см; y3 = 20 см. Положение центра тяжести представленного сечения определяем по формуле
хс = (1 200 ∙ 15 + 1 000 ∙ 46,7 – 628 ∙ 8,5) / (1 200 + 1 000 – 628) = 37,8 см.
yc = 15,7 см.
РАЗДЕЛ II. КИНЕМАТИКА ВВЕДЕНИЕ Кинематикойназывается раздел механики, в котором изучается движение материальных точек и тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение. Мы будем изучать простейшую форму движения – механическое движение, т. е. происходящее во времени изменение положения одного тела относительно другого, с которым связана система координат, называемая системой отсчета. Эта система может быть как движущейся, так и условно неподвижной. Рассматривая движение, мы связываем изменение положения тела с течением времени. При изучении движения всегда устанавливаем начало отсчета времени Непрерывную кривую, которую описывает точка при своем движении, называют траекторией. Если траектория движения – прямая линия, то движение называется прямолинейным, если кривая – криволинейным. ДВИЖЕНИЕ ТОЧКИ Способ задания движения Задать движение точки по отношению к избранной системе отсчета – это значит указать способ, при помощи которого можно определить положение точки в любой момент времени. Существуют три способа задания движения. 1. Векторный способ. Положение точки в пространстве однозначно определяется заданием радиуса-вектора Для определения движения точки нужно знать, как изменяется с течением времени
Рис. 2.1
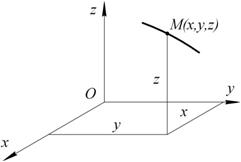
Годографом какого-либо вектора называют кривую, которую вычерчивает конец этого вектора при изменении его аргумента (предполагается, что начало вектора, находится в одной и той же точке). Таким образом, годографом радиуса-вектора является траектория точки. 2. Координатный способ. Положение точки М в системе координат Оху определяется координатами х, y, z (рис. 2.2).
Рис. 2.2 При движении точки М ее координаты изменяются с течением времени. Следовательно, координаты х, y, z движущейся точки, являются функциями времени Эти уравнения называются уравнениями движения точки в декартовых координатах. Пусть движение точки М в плоскости задано уравнениями:
Из первого уравнения выразим время Полученная зависимость есть уравнение траектории точки. 3. Естественный способ задания движения. Этот способ применяется в том случае, если траектория точки заранее известна (рис. 2.3). Выберем на траектории неподвижную точку О, которую назовем началом отсчета дуговой координаты. Рис. 2.3 дуговой координаты. При движении точки М
расстояние S от этой точки до неподвижной точки О изменяется с течением времени:
Выражение (2.3) является уравнением движения точки М.
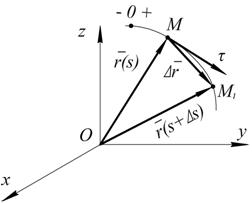
Скорость точки 1. Векторный способ задания движения. Пусть в момент времени Вектор
Рис. 2.4
Скоростью точки в данный момент времени называется предел отношения вектора перемещения точки к промежутку времени, за которое произошло это перемещение, при стремлении этого промежутка времени к нулю: Скорость точки – это вектор, направленный по касательной к траектории в сторону движения. 2. Координатный способ задания движения. Пусть движение точки задано как Тогда для радиуса-вектора точки М можно записать: где Согласно (2.5) Дифференцируем (*)
С другой стороны, для вектора где Сравнивая (**) и (***), получим: Модуль скорости точки Направление скорости определяется направляющими косинусами:
3. Естественный способ задания движения.
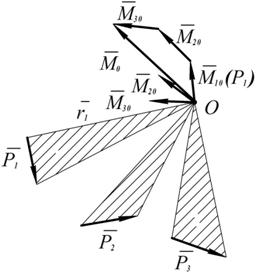
Согласно (2.5)
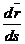 : :
Вектор При Обозначим единичный орт касательной через
Таким образом, Равенство (*) примет вид
Модуль
2.3. Ускорение точки 1. При векторном способе задания движения: Предположим, что в момент времени Предел приращения скорости к приращению времени, за которое произошло это приращение, при условии, что 2. При координатном способе задания движения: Вектор скорости точки С учетом (2.9) Но для вектора ускорения точки имеем: Сравнивая (*) и (**), получим:
Модуль ускорения точки Направление вектора ускорения определяется направляющими косинусами:
3. При естественном способе задания движения: Пусть известна траектория точки. Возьмем две близкие на траектории точки М и М1 – Вектор Плоскость, перпендикулярная соприкасающейся, называется нормаль-ной. Плоскость, перпендикулярная нормальной и соприкасающейся плоскостям, называется спрямляющей (рис. 2.6).
Рис. 2.6
Три взаимно перпендикулярные плоскости: нормальная, соприкасающаяся и спрямляющая – образуют естественный трехгранник. Линия пересечения нормальной и соприкасающейся плоскостей называется главной нормалью. Орт главной нормали – Три взаимно перпендикулярные оси: касательная, направленная в сторону возрастания дуговой координаты; главная нормаль, направленная в сторону вогнутости траектории; бинормаль, направленная по отношению к Угол между касательными в двух ближайших точках траектории называется углом смежности: Кривизной кривой в точке М называется предел отношения угла смежности к абсолютному значению длины дуги ММ1, между ближайшими точками траектории Радиусом кривизны в точке М называется величина, обратная кривизне:
Получим формулу для вычисления ускорения точки М. Согласно выражению (2.8) имеем: Продифференцируем по времени обе части этого равенства:
Вычислим:
Так как направление по главной нормали, то Подставим в (*):
Ускорение точки лежит в соприкасающейся плоскости и определяется как векторная сумма касательного и нормального ускорений точки: Проекция ускорения на касательную определяется формулой Касательное ускорение характеризует изменение скорости по величине. Оно равно нулю, когда величина скорости остается неизменной. Кроме того, оно обращается в нуль в те моменты времени, когда скорость достигает экстремальных значений. Величина нормального ускорения определяется выражением где Нормальное ускорение характеризует изменение скорости
Рис. 2.7
Направление ускорения
Некоторые частные случаи движения точки 1. Прямолинейное движение. Так как при прямолинейном движении скорость изменяется только численно, то делаем вывод, что касательное ускорение характеризует изменение скорости по численной величине. 2. Равномерное криволинейное движение. Равномерным называется такое движение, в котором численная величина скорости остается все время постоянной (
Так как ускорение при равномерном движении появляется в результате изменения направления скорости, то нормальное ускорение характеризует изменение скорости по направлению. Получим закон движения: Отсюда Проинтегрируем: Подставим пределы интегрирования: В результате получим закон равномерного криволинейного движения:
3. Равномерное прямолинейное движение. следовательно, 4. Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение, при котором касательное ускорение остается величиной постоянной: Проинтегрируем: но Тогда
|
||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 690. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
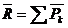 .
.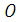 :
:
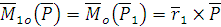 ;
;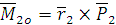 ;
;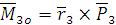 .
.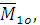
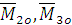 приложены в точке
приложены в точке 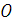 . Построим многоугольник векторов моментов. Замыкающая сторона этого многоугольника – главный момент относительно неподвижного центра
. Построим многоугольник векторов моментов. Замыкающая сторона этого многоугольника – главный момент относительно неподвижного центра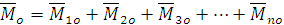
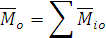
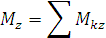
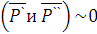 , причём
, причём 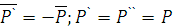 .
.
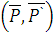 образуют пару, момент которой
образуют пару, момент которой 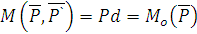 .
.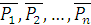 . Геометрическая сумма этих сил есть главный вектор
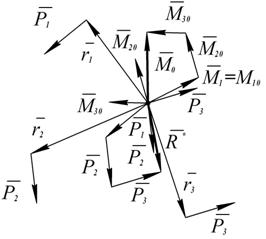
. Геометрическая сумма этих сил есть главный вектор 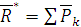 .
.
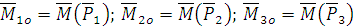 также образуют систему сходящихся векторов. Их геометрическая сумма есть главный момент системы сил относительно центра
также образуют систему сходящихся векторов. Их геометрическая сумма есть главный момент системы сил относительно центра 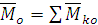 .
.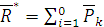 .
.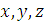 (рис. 1.47).
(рис. 1.47).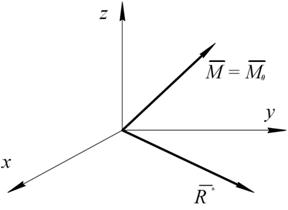
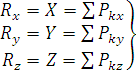 .
.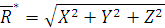 .
.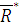 определяется направ-лением косинусов:
определяется направ-лением косинусов: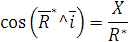
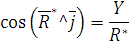
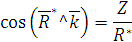
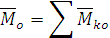 .
.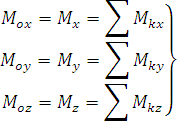 .
.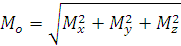 .
.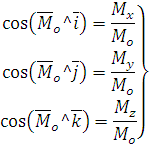
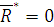 , система сходящихся сил, приложенных в центре приведения эквивалентна нулю, а при
, система сходящихся сил, приложенных в центре приведения эквивалентна нулю, а при 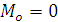 - система пар сил эквивалентна нулю. Следовательно, исходная система сил эквивалентна нулю.
- система пар сил эквивалентна нулю. Следовательно, исходная система сил эквивалентна нулю.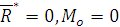 .
.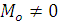 , и, следовательно, она не является уравновешенной, что противоречит исходной предпосылке.
, и, следовательно, она не является уравновешенной, что противоречит исходной предпосылке.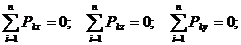
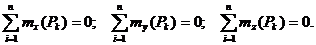
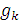 приложены в их центрах (рис.1.49).
приложены в их центрах (рис.1.49).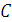 ;
; 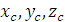 – координаты центра тяжести
– координаты центра тяжести 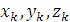 – координаты центров тяжести частей тела.
– координаты центров тяжести частей тела.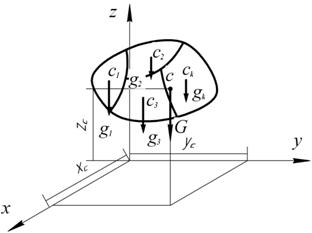
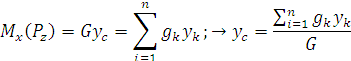
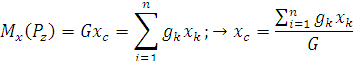
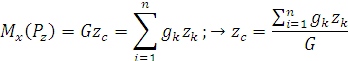
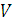 :
: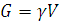 ,
,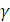 – вес единицы объёма.
– вес единицы объёма.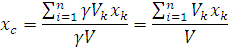 ,
,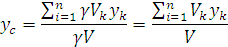 ,
,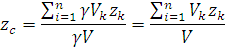 ,
,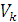 – объём элемента тела;
– объём элемента тела;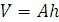 ,
,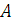 – площадь фигуры;
– площадь фигуры;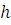 – её высота.
– её высота.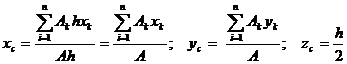 ,
,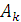 – площадь части сечения;
– площадь части сечения;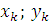 – координаты центра тяжести частей сечения.
– координаты центра тяжести частей сечения.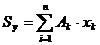 называют статическим моментом
называют статическим моментом 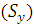 относительно оси y.
относительно оси y.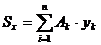 – статический момент относительно оси х.
– статический момент относительно оси х.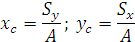 .
.
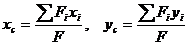 .
.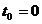 .
.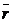 , проведенного из некоторого неподвижного центра О в данную точку М (рис. 2.1).
, проведенного из некоторого неподвижного центра О в данную точку М (рис. 2.1).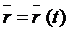 . (2.1)
. (2.1)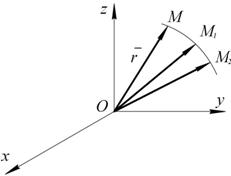
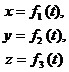 . (2.2)
. (2.2)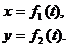
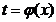 и подставим во второе:
и подставим во второе: 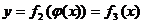 .
.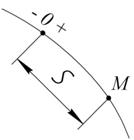 Положение точки М на траектории будем определять дуговой координатой S, отложенной на траектории от начала отсчета О. Расстояния, отложенные в одну сторону от точки О, будем считать положительными, в другую – отрицательными, т. е. установим направление отсчета
Положение точки М на траектории будем определять дуговой координатой S, отложенной на траектории от начала отсчета О. Расстояния, отложенные в одну сторону от точки О, будем считать положительными, в другую – отрицательными, т. е. установим направление отсчета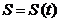 , (2.3)
, (2.3)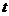 положение точки М определяется
положение точки М определяется 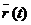 , а в момент
, а в момент 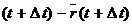 (рис. 2.4).
(рис. 2.4).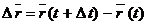 будем называть вектором перемещения точки за время
будем называть вектором перемещения точки за время 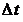 . Отношение
. Отношение 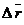 к
к 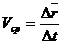 . (2.4)
. (2.4)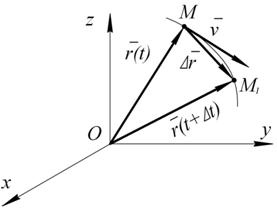
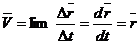 . (2.5)
. (2.5)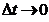
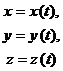 .
.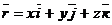 , (*)
, (*)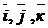 – единицы орты осей х, y, z.
– единицы орты осей х, y, z.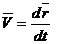 .
. 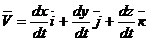 . (**)
. (**)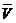 справедливо соотношение
справедливо соотношение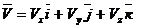 , (***)
, (***)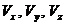 – проекции
– проекции 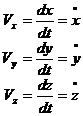 (2.6)
(2.6)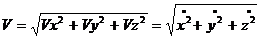 (2.7)
(2.7)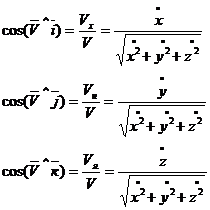
 Пусть в момент времени t положение точки М определяется координатой S в момент
Пусть в момент времени t положение точки М определяется координатой S в момент 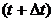 –
– 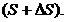 (рис. 2.5).
(рис. 2.5).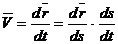 . (*)
. (*)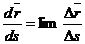 .
.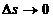
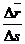 направлен так же, как
направлен так же, как 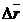 .
.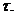
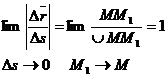 ,
,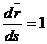 , следовательно,
, следовательно, 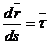 , так как
, так как 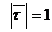 .
.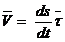 . (2.8)
. (2.8)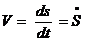 , направление
, направление 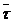 .
.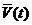 , а в момент
, а в момент 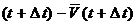 .
.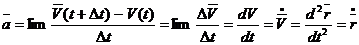 (2.9)
(2.9)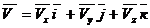 .
.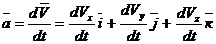 (*)
(*)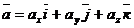 . (**)
. (**)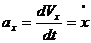
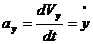 (2.10)
(2.10)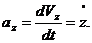
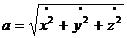 . (2.11)
. (2.11)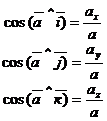
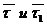 .
. перенесем в точку М и проведем плоскость через
перенесем в точку М и проведем плоскость через 
 . Линия пересечения нормальной и спрямляющей плоскостей называется бинормалью траектории. Ось бинормали
. Линия пересечения нормальной и спрямляющей плоскостей называется бинормалью траектории. Ось бинормали 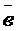 .
.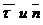 так же, как ось z по отношению к осям х, y, – называются естественными осями.
так же, как ось z по отношению к осям х, y, – называются естественными осями.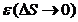 .
.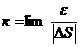 (2.12)
(2.12)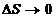
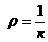 . (2.13)
. (2.13)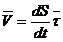 .
.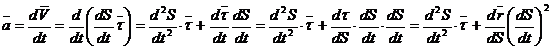 (*)
(*)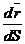 .
. 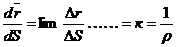 .
.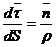 .
.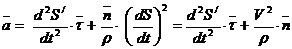 .
.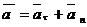 . (2.14)
. (2.14)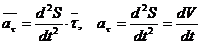 . (2.15)
. (2.15)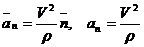 , (2.16)
, (2.16)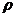 – радиус кривизны.
– радиус кривизны.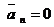 в точках,
в точках, 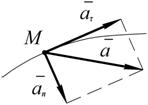 Модуль ускорения (рис. 2.7) вычисляется по формуле
Модуль ускорения (рис. 2.7) вычисляется по формуле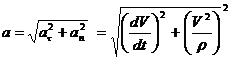 . (2.17)
. (2.17)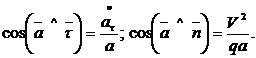
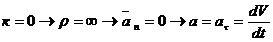 .
.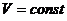 ):
):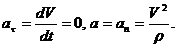
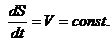
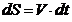 .
.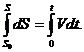
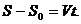
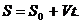
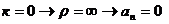
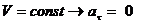 ,
,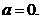
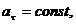
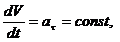
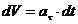 .
.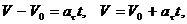
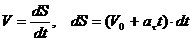 .
. 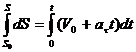 .
.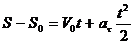 .
.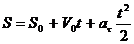 – закон равнопеременного криволинейного движения.
– закон равнопеременного криволинейного движения.