
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Момент силы относительно точки. Момент силы относительно оси. Теория пар в пространствеВ случае плоской системы сил момент силы относительно точки определён как алгебраическая величина:
Рис. 1.40
Модуль вектора
Моментом силы относительно оси называется скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью (1.41).
Рис. 1.41
Если сила Итак, момент силы относительно точки – вектор, а момент силы относительно оси – скалярная величина. При вычислении моментов относительно оси надо иметь в виду следующие частные случаи: 1. Если сила параллельна оси, то её момент относительно оси равен нулю 2. Если линия действия силы пересекает ось, то её момент относительно оси равен нулю 3. Если сила перпендикулярна оси, то её момент относительно оси равен произведению модуля силы на расстояние между силой и осью. Аналитическое выражение для моментов силы относительно осей координат получим следующим образом.  Спроецируем силу Тогда
Последнее равенство вытекает из теоремы Вариньона. Но, как видно из чертежа,
Рис. 1.42
В результате получим:
Зависимость между моментом силы относительно центра и относительно оси Пусть на тело действует приложенная в точке
 относительно центра будет изображаться вектором относительно центра будет изображаться вектором  , перпендикулярным плоскости , перпендикулярным плоскости 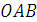 , причём по модулю , причём по модулю
Проведём теперь через любую точку
Но треугольник Умножим обе части уравнения на 2, находим:
Произведение
Рис. 1.43
Момент силы
|
||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 401. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . При пространственном расположении сил этого определения недостаточно, так как плоскости, проходящие через линии действия сил, и точка, относительно которой определяется момент, различны. Поэтому момент
. При пространственном расположении сил этого определения недостаточно, так как плоскости, проходящие через линии действия сил, и точка, относительно которой определяется момент, различны. Поэтому момент  силы P относительно точки О в пространстве определяют как векторное произведение
силы P относительно точки О в пространстве определяют как векторное произведение 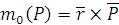 , где
, где 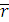 – вектор-радиус, проведенный из точки О в точку приложения силы (рис. 1.40).
– вектор-радиус, проведенный из точки О в точку приложения силы (рис. 1.40). Таким образом, вектор
Таким образом, вектор  направлен перпендикулярно плоскости, содержащей линию действия силы и точку О, так, что сила
направлен перпендикулярно плоскости, содержащей линию действия силы и точку О, так, что сила  с конца вектора
с конца вектора  .
. .
.
 с конца оси z направлена против часовой стрелки, то момент считается положительным.
с конца оси z направлена против часовой стрелки, то момент считается положительным.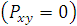 .
. .
.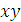 и разложим полученную проекцию на составляющие
и разложим полученную проекцию на составляющие  и
и 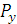 ; численно эти составляющие будут, очевидно, равны проекциям силы
; численно эти составляющие будут, очевидно, равны проекциям силы  (рис. 1.42).
(рис. 1.42). .
. , следовательно,
, следовательно,  . Аналогично вычисляются моменты относительно других осей.
. Аналогично вычисляются моменты относительно других осей.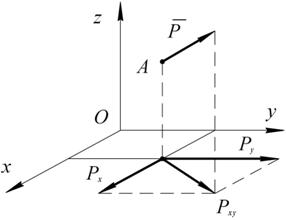
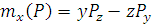 ,
, ,
,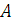 сила
сила  и возьмем на ней произвольную точку
и возьмем на ней произвольную точку 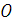 .
. .
.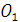 плоскость
плоскость  .
.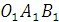 представляет собой проекцию треугольника
представляет собой проекцию треугольника 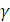 . Тогда
. Тогда  .
. ,
, даёт проекцию
даёт проекцию  или
или  .
.