
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Приведение плоской системы сил к данному центруПусть на твёрдое тело действует какая-нибудь система сил
Рис. 1.37
В результате на тело будут действовать: система сил
и система пар сил, моменты которых равны:
Силы, приложенные в центре О, можно заменить одной силой
Главным вектором
Проекции главного вектора на координатные оси равны суммам проекций слагаемых сил:
Модуль главного вектора
Направляющие главного вектора:
Главным моментом
Итак, мы показали, что всякая плоская система сил, действующая на абсолютно твёрдое тело, при приведении к произвольному центру О заменяется одной силой
Условия равновесия произвольной плоской системы сил Для равновесия любой плоской системы необходимо и достаточно, чтобы одновременно выполнялось условие:
1. Основная форма записи условия равновесия Величины
где
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы всех сил на каждую из двух координатных осей и суммы их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.  2. Вторая форма записи условий равновесия. Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось Оx не перпендикулярную к прямой АВ, были равны нулю:
2. Третья форма
Должно соблюдаться условие, что А, В, С не лежат на одной прямой.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ Системы сходящихся сил Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник. В отличие от соответственно плоской задачи силовой многоугольник не является плоским, т. е. он представляет ломаную пространственную линию. Проекции равнодействующей силы R на оси декартовых координат x, y, z равны суммам проекций слагаемых сил на соответствующей оси (рис. 1.38).
Рис. 1.38
Модуль равнодействующей (рис. 1.39)
Направляющие косинусы
Рис. 1.39
Для равновесия твердого тела, к которому приложена пространственная система сходящихся сил, необходимо и достаточно, чтобы равнодействующая равнялась нулю, т. е. чтобы силовой многоугольник был замкнут. При этом уравнения равновесия имеют вид
Произвольная пространственная система сил |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 409. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
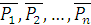 . Возьмём в этой плоскости произвольную точку О, которую назовём центром приведения, и перенесём все силы в центр О (рис. 1.37).
. Возьмём в этой плоскости произвольную точку О, которую назовём центром приведения, и перенесём все силы в центр О (рис. 1.37).

 .
. , при этом
, при этом 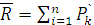 или
или 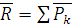 . Согласно теореме о сложении пар, все пары можно заменить одной парой:
. Согласно теореме о сложении пар, все пары можно заменить одной парой: или
или  .
.
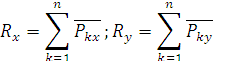 .
.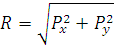 .
. ;
; .
. относительно центра О называется сумма моментов сил, приложенных к твёрдому телу, относительно этого центра
относительно центра О называется сумма моментов сил, приложенных к твёрдому телу, относительно этого центра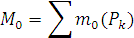
 .
.
 .
. может равняться нулю только тогда, когда одновременно
может равняться нулю только тогда, когда одновременно 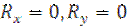 . Следовательно, условия равновесия будут выполняться, если
. Следовательно, условия равновесия будут выполняться, если .
. .
. .
.
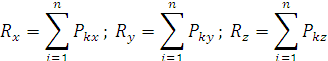
 .
. .
.
