
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Равновесие твёрдого тела при наличии плоской системы сил. Случай параллельных силРавнодействующая двух параллельных сил, направленных в одну сторону, равна по модулю сумме модулей слагаемых сил и направлена в ту же сторону. Линия действия равнодействующей делит внутренним образом расстояние между линиями действия слагаемых сил на части, обратно пропорциональные этим силам (рис. 1.29):
Рис. 1.29
Равнодействующая, двух параллельных сил, неравных по модулю
Рис. 1.30
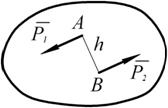
Система двух параллельных сил, равных по модулю и направленных в разные стороны, называется парой сил (рис. 1.31).
h – плечо пары.
Рис. 1.31 Так как две силы, равные по модулю и направленные в разные стороны, не лежат на одной линии действия, то твёрдое тело, к которому приложена пара сил, не находится в равновесии. Пара сил стремится повернуть твёрдое тело, к которому она приложена. Мерой действия пары сил является алгебраическая величина, называемая моментом. Момент пары сил равен по абсолютной величине произведению модуля одной из сил пары и плеча (рис. 1.32 и 1.33).
Рис. 1.32 Рис. 1.33
Теория пар сил на плоскости сводится к трем теоремам. Теорема 1. Не нарушая состояния твёрдого тела, пару сил можно переносить в плоскости её действия.  Теорема 2. Пара сил, моменты которых равны, эквивалентны (пары сил называются эквивалентными, если одну из пар можно заменить другой, не нарушая состояния твёрдого тела) (рис. 1.34). Это значит, что, не нарушая состояния твёрдого тела, можно изменить величину либо плеча, либо силы, сохраняя при этом неизменным момент пары сил.
Рис. 1.34
Теорема 3 (сложение пар сил на плоскости). При сложении нескольких пар сил на плоскости получается равнодействующая пара, момент m которой равен сумме моментов слагаемых пар (рис. 1.35):
Рис. 1.35
Для равновесия твёрдого тела под действием пары сил, лежащих в одной плоскости, необходимо и достаточно, чтобы сумма моментов слагаемых пар равнялась нулю:
Теорема о параллельном переносе силы Силу, приложенную к твёрдому телу, можно не изменяя оказываемого действия, переносить параллельно ей самой в любую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится. Пусть на твёрдое тело, действует сила
|
||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 411. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
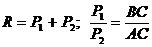 .
.
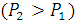 и направленных в разные стороны, равна по модулю разности модулей этих сил и направлена в сторону большей силы. Линия действия равнодействующей делит внешним образом расстояние между линиями действия слагаемых сил на части обратно пропорционально этим силам (рис. 1.30).
и направленных в разные стороны, равна по модулю разности модулей этих сил и направлена в сторону большей силы. Линия действия равнодействующей делит внешним образом расстояние между линиями действия слагаемых сил на части обратно пропорционально этим силам (рис. 1.30). ;
;  .
.





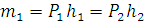

 ;
; ;
; .
.


 в точке А (рис. 1.36). Действие этой силы, не изменится, если в любой точке В, приложить две уравновешивающиеся силы
в точке А (рис. 1.36). Действие этой силы, не изменится, если в любой точке В, приложить две уравновешивающиеся силы  и
и 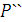 . Полученная система трёх сил и представляет собой силу
. Полученная система трёх сил и представляет собой силу  , но приложенную в точке В и
, но приложенную в точке В и  с моментом
с моментом  .
.

