
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Равновесие твёрдого тела, к которому приложена система сходящихся силСтр 1 из 35Следующая ⇒ Тверской государственный технический университет В.В. ГАРАНИКОВ ТЕХНИЧЕСКАЯ МЕХАНИКА Теоретическая механика Учебное пособие
Издание первое
Тверь 2013 УДК 539.3.6(075.8) ББК 30.121я7 Гараников, В.В. Техническая механика. Теоретическая механика: учеб. пособ. / В.В. Гараников. Тверь: ТвГТУ, 2013. 116 с. Изложен один из разделов дисциплины «Механика» – курс теоретической механики. Объем представленного материала соответствует программе дисциплины «Техническая механика», рекомендованной для данного направления подготовки бакалавров Министерством образования и науки Российской Федерации и учебному плану. Дисциплина «Техническая механика» является обще-профессиональной, обеспечивающей базовые знания при усвоении специальных дисциплин, изучаемых в дальнейшем. Книга предназначена для студентов, изучающих данный раздел механики, рекомендуется также для студентов заочной формы обучения и ИДПО.
Рецензенты: Член национального комитета по теоретической и прикладной механике, зав. кафедрой «Строительство, стройматериалы и конструкции» Тульского государственного университета, советник РААСН, доктор технических наук, профессор Трещев А.А.; зав. кафедрой механизации природоустройства и ремонта машин Тверского государственного технического университета, профессор, доктор технических наук Фомин К.В.
© Тверской государственный технический университет, 2013
 ПРЕДИСЛОВИЕ
Учебная дисциплина «Техническая механика» состоит из трех разделов: «Теоретическая механика», «Сопротивление материалов», «Детали машин». Согласно учебным планам для ряда специальностей раздел «Детали машин» изучается отдельно. Автором ставилась задача в сжатой и доступной форме изложить основные положения только одного раздела учебной дисциплины, а именно теоретической механики, которому согласно учебным планам выделяется только один семестр. РАЗДЕЛ I. СТАТИКА ТВЕРДОГО ТЕЛА ОСНОВНЫЕ ПОНЯТИЯ СТАТИКИ Введение Теоретическая механика – это наука, в которой изучаются общие законы механического движения и механического взаимодействия материальных тел. Механическим движением называется изменение с течением времени взаимного положения материальных точек в пространстве. Механическое взаимодействие – это взаимодействие материальных тел, изменяющее характер их механического движения. Курс теоретической механики делится на три раздела: статику, кинематику и динамику. Статика– это раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому телу. Кинематика– раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение. Динамика – раздел механики, в котором изучается движение материальных тел в пространстве в зависимости от действующих на них сил. Материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать, называют материальной точкой. Материальная точка обладает массой и способностью взаимодействовать с другими телами. В теоретической механике рассматривают тела, расстояние между точками которых остаются неизменными. Такие тела называются абсолютно твердыми. Принимаем эту модель в качестве объекта исследования, пренебрегая возможными изменениями формы и размеров тела под действием нагрузок, а также полагая: 1) что деформации малы – ими можно пренебречь; 2) условие равновесия сил, приложенных к абсолютно твердому телу, является необходимым условием равновесия любого тела. Одним из важнейших в теоретической механике является понятие силы. Сила– это мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия. Сила обозначается вектором (рис.1.1).
Рис. 1.1
Сила определяется тремя элементами: числовым значением, направлением, точкой приложения; измеряют ее в ньютонах. Совокупность нескольких сил, действующих на данное тело, называют системой сил:
Если, не нарушая состояния тела, одну систему сил
В том случае, когда система сил Если абсолютно твердое тело останется в состоянии покоя при действии на него системы сил
Часто в этом случае говорят, что тело находится в равновесии. Силы, действующие на материальную систему, делятся на две группы: внешние и внутренние. Внешними называются силы, действующие на материальные точки данной системы со стороны материальных точек (тел), не принадлежащих этой системе; внутренними – силы взаимодействия между материальными точками рассматриваемой системы (силы межмолекулярного сцепления).
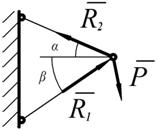
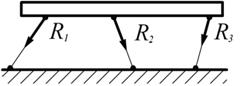
Различают силы: сосредоточенные, которые передаются через небольшую площадь или можно сказать в точке (рис. 1.2); распределённые – действуют через определённую площадь или, можно считать, точку (рис. 1.3).
Рис. 1.2 Рис.1.3
Аксиомы статики Аксиомы статики сформулированы на основе наблюдения и изучения окружающих нас явлений реального мира. Некоторые основные законы механики Галилея – Ньютона являются одновременно и аксиомами статики. 1. Аксиома инерции. Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно. Равномерное и прямолинейное движение материальной точки является движением по инерции. 2. Аксиома равновесия двух сил. Две силы, приложенные к телу, взаимно уравновешиваются только в том случае, если их модули равны и они направлены по одной прямой в противоположные стороны (рис. 1.4).
Рис. 1.4
3. Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на твёрдое тело не изменяется, если к ней присоединить или из неё исключить систему взаимно уравновешивающихся сил (рис. 1.5).
Рис. 1.5
Пусть к твёрдому телу приложены силы Следствие. Не нарушая состояния абсолютно твёрдого тела, силу можно переносить вдоль линии её действия, сохраняя неизменными её модуль и направление (рис. 1.6).
Рис. 1.6
Предположим, в точке А приложена Таким образом, силу можно переносить в любую точку по линии действия, не изменяя её модуля и направления, поэтому в статике сила рассматривается как скользящий вектор.
4. Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах (рис. 1.7).
Рис. 1.7
5. Аксиома равенства действия и противодействия. Всякому действию соответствует равное и противоположно направленное противодействие. Эта аксиома утверждает, что силы действия друг на друга двух сил равны по модулю и направлены в противоположные стороны. Аксиома установлена Ньютоном (рис. 1.8 и 1.9).
Рис. 1.8 Рис. 1.9
В природе не существует одностороннего действия сил. Силы, действующие и противодействующие, приложены к разным телам, потому они не уравновешиваются. 6. Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердевании. Равновесие сил, приложенных к деформирующемуся телу, сохраняется при его затвердении. Из этой аксиомы следует, что условие равновесия сил, приложенных к абсолютно твёрдому телу, должно сохраняться и для сил, приложенных к деформирующемуся телу. Однако в случае деформированного тела эти условия необходимы, но не достаточны (рис. 1.10).
Рис. 1.10
Несвободное твёрдое тело Твёрдое тело, на перемещение которого не наложено никаких ограничений, называется свободным. Тело, ограничивающее свободу движения данного твёрдого тела, является по отношению к нему связью. Твёрдое тело, свобода движения которого ограничена связями, называется несвободным. Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождаемости твёрдых тел от связей). Все связи можно разделить на несколько типов: 1. Идеально гладкая поверхность. Реакции опоры, приложенные в точке опоры, всегда направлены перпендикулярно ей (рис. 1.11).
Рис. 1.11
2. Гибкая связь (трос, нить, цепь, канат). Реакция гибкой нити направлена по нити к точке подвеса (рис. 1.12).
Рис. 1.12 . 3. Жёсткий стержень. На схемах показывается толстой линией
Рис. 1.13
4. Брус (рис. 1.14).
Рис. 1.14
5. Цилиндрическая шарнирно-неподвижная опора (рис. 1.15).
Рис. 1.15
6. Цилиндрическая шарнирно-подвижная опора (рис. 1.16).
Рис. 1.16
7. Защемление (заделка) (рис. 1.17).
Рис. 1.17
8. Невесомый стержень, на концах которого шарниры (рис. 1.18).
Рис. 1.18
9. Сферический шарнир (рис. 1.19).
Рис. 1.19
10. Подпятник – совокупность цилиндрического шарнира и упорной поверхности (рис. 1.20).
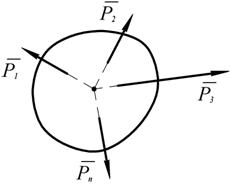
Рис. 1.20 ПЛОСКАЯ СИСТЕМА СИЛ Система сходящихся сил Равновесие твёрдого тела, к которому приложена система сходящихся сил Сходящимися называются силы, линии действия которых пересекаются в одной точке. Теорема. Система сходящихся сил эквивалентна общей силе – равнодействующей, которая равна геометрической сумме этих сил и проходит через точку пересечения их линий действия (рис. 1.21):
Согласно следствию из аксиомы 3 перенесём точки приложения сил по линиям их действия в точку пересечения этих линий. Она эквивалентна исходной системе сходящихся сил. Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма (аксиома 4).
Равнодействующая
Рис. 1.21 Рис. 1.22
Строим силовой многоугольник: от конца
Рис. 1.23
Обе части (1.1) спроектируем на оси x, y, z.
Модуль равнодействующей
Направление равнодействующей определяется направляющимися косинусами:
где i, j, k – единичные орты осей x, y, z. Для равновесия твёрдого тела, к которому приложена система сходящихся сил, необходимо и достаточно, чтобы векторная сумма этих сил равнялась нулю:
Рис. 1.24
Равенство
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы алгебраические проекции всех сил данной системы на координаты осей x, y, z равнялись нулю. Для плоской системы сходящихся сил система принимает вид
|
|||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 462. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 © Гараников В.В., 2013
© Гараников В.В., 2013

 можно заменить другой
можно заменить другой  и наоборот, то такие системы сил называются эквивалентными:
и наоборот, то такие системы сил называются эквивалентными: .
. эквивалентна одной силе
эквивалентна одной силе  , т. е.
, т. е.  , то последняя называется равнодействующей этой системы сил.
, то последняя называется равнодействующей этой системы сил. .
.

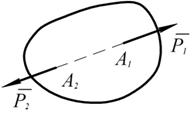

 , под действием которых тело находится в покое или совершает какое-то движение. Приложим к телу равные противоположно направленные силы
, под действием которых тело находится в покое или совершает какое-то движение. Приложим к телу равные противоположно направленные силы  и
и  , которые взаимно уравновешиваются.
, которые взаимно уравновешиваются.  Если тело находится в движении, то оно будет двигаться под действием новой системы сил
Если тело находится в движении, то оно будет двигаться под действием новой системы сил 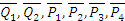 так же, как и под действием сил
так же, как и под действием сил 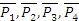 , т. е. основная система сил эквивалентна прежней.
, т. е. основная система сил эквивалентна прежней.
 . Приложим в точке В две
. Приложим в точке В две 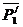 и
и  , равные по модулю силе
, равные по модулю силе 














 ;
; ;
; . (1.1)
. (1.1)
 отложим
отложим  , от его конца
, от его конца  и т. д. Затем соединяем начало первого вектора с концом последнего. Последний вектор и есть
и т. д. Затем соединяем начало первого вектора с концом последнего. Последний вектор и есть  .
.

 (1.2)
(1.2)
 (1.3)
(1.3) ,
, ,
,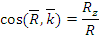 ,
, (*). Это означает, что в силовом многоугольнике уравновешенной системы сходящихся сил конец последней силы должен совпадать с началом первой, т. е. многоугольник замкнут (рис. 1.24).
(*). Это означает, что в силовом многоугольнике уравновешенной системы сходящихся сил конец последней силы должен совпадать с началом первой, т. е. многоугольник замкнут (рис. 1.24).

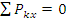

 (1.4)
(1.4) или
или 