
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
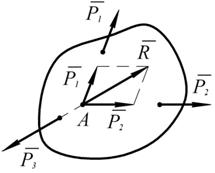
Теорема о трех непараллельных силахЕсли исходное тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. Доказательство: Пусть на тело действует система трех сил
Рис. 1.25
Таким образом, рассматриваемая система сил приведена к двум Момент силы относительно точки Опыт показывает, что под действием силы твёрдое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется её моментом. Моментом силы относительно центра называется вектор, равный векторному произведению радиуса-вектора точки приложения силы на вектор силы (рис. 1.26).
Рис. 1.26
Вектор – момент силы Модуль векторного произведения равен площади параллелограмма, построенного на векторных сомножителях. Его модуль равен
В общем случае момент силы относительно центра алгебраически равен взятому со знаком «+» или «–» произведению модуля силы на плечо силы:
Знак «+» выбираем в том случае, если кратчайший поворот силы вокруг данного центра виден происходящим против часовой стрелки  Момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку, так как при этом плечо равно нулю.
Рис. 1.27 Теорема Вариньона Теорема Вариньона для системы сходящихся сил гласит: момент относительно точки равнодействующей
Удобство данной теоремы заключается в том, что, минуя непосредственное определение равнодействующей, можно вычислить её момент относительно точки, зная моменты всех слагаемых сил относительно той же точки. Пусть а, b – координаты точки А (1.28).
Рис. 1.28
Тогда
где x, y – координаты точки В. Этой формулой рекомендуется пользоваться в тех случаях, когда определение величины h связано с вычислительными трудностями.
Произвольная плоская система сил |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 563. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , причём линии действия
, причём линии действия  и
и  пересекаются в точке А, согласно аксиоме 4 их можно заменить одной
пересекаются в точке А, согласно аксиоме 4 их можно заменить одной  (рис.1.25):
(рис.1.25): .
.
 и
и  . По условиям теоремы тело находится в равновесии, следовательно, по аксиоме 2 силы
. По условиям теоремы тело находится в равновесии, следовательно, по аксиоме 2 силы  . (1.6)
. (1.6)
 относительно точки О приложен в ней.
относительно точки О приложен в ней.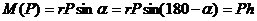 ,
, .
. .
.
 равен сумме моментов слагаемых сил относительно той же точки:
равен сумме моментов слагаемых сил относительно той же точки: .
.
 ,
, – проекции силы
– проекции силы  на координатные оси;
на координатные оси;