
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Проверка статистических гипотез.⇐ ПредыдущаяСтр 14 из 14
Одна из часто встречающихся на практике задач состоит в том, должно ли на основании данной выборки быть принято или опровергнуто некоторое предположение (гипотеза) относительно генеральной совокупности (случайной величины). Под статистической гипотезой понимается всякое предположение о генеральной совокупности. Стат гипотезы делятся на:1)гип-зы о параметрах распределения известного вида, 2) гип-ps о виде неизвестного распр-я. Обычно выдвигают нулевую гип-зу Но (основную) и альтернативную ей Н1 (конкурирующую). Простая гип-за - гип-за, однозначно фиксирующая распределение наблюдений. В ней идет речь об одном значении параметра, иначе- сложная гип-за. Этапы проверки статистических гипотез 1. Формулировка основной гипотезы H0 и конкурирующей гипотезы H1. Гипотезы должны быть чётко формализованы в математических терминах. 2. Задание вероятности α, называемой уровнем значимости и отвечающей ошибкам первого рода, на котором в дальнейшем и будет сделан вывод о правдивости гипотезы. 3. Расчёт статистики φ критерия такой, что: её величина зависит от исходной выборки § по её значению можно делать выводы об истинности гипотезы H0; § сама статистика φ должна подчиняться какому-то известному закону распределения, т.к. сама φ является случайной в силу случайности 4. Построение критической области. Из области значений φ выделяется подмножество  5. Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику φ и по попаданию (или непопаданию) в критическую область
Основные методы определения точечных оценок. 1. Метод моментов (аналогии) К. Пирсен в 1894. Идея метода: для нахождения оценок неизвестных параметров распре-я теорит. начальные моменты следует приравнять к эмпирическим нач. моментам того же порядка. Решая полученное Ур-е или систему Ур-ний находим оценку неизв. параметров распределения. Получ. оценки явл-ся сст-мы, но малоэф., т.е. явл-ся грубыми оценками. 2. Метод макс. правдоподобия. Этот метод по сравнению с методом моментов явл-ся более сложым и точным.Он может быть использован для малых выборок. В основе этого метода лежит функц. макс. правдоподобия. 1). Х-ДСВ с законом Р(Х=Хi,
Из опред-я метода Св-ва: 1. Оценка макс. правдоподобия явл-ся состоятельной. 2. Оценка макс. правдоподобия им. норм. асимпт. распред-е. 3. Решение Ур. правдоподоб. единственно. 4. Оценка макс. прадоподобия эф-на при
3. Другие методы. -метод наим. квадратов -метод наим. абс. откл-й -метод наим. макс.отклонения Кажд. из указ. методов сущ-ет сам-но и обладает преим-м перед остальными.Основой этих методов явл-ся метод макс. правдоподобия.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 278. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ;
; .
. таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство
таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство  . Это множество
. Это множество 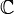 и называется критической областью.
и называется критической областью.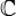 выносится решение об отвержении (или принятии) выдвинутой гипотезы H0.
выносится решение об отвержении (или принятии) выдвинутой гипотезы H0. )=р(Хi,
)=р(Хi,  )
) 2). Х-НСВ, f(Xi,
2). Х-НСВ, f(Xi,  Суть метода состоит в том, чтобы найти из множества значений неизв. парам.
Суть метода состоит в том, чтобы найти из множества значений неизв. парам.  такое значение
такое значение 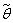 , кот. максимизировало бы функцию правдоподобия.
, кот. максимизировало бы функцию правдоподобия. чем правдоподобнее при фиксир.
чем правдоподобнее при фиксир. 

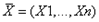 набор или выборка, тем больше, чем знач. ф-ии
набор или выборка, тем больше, чем знач. ф-ии 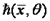 . Отсюда и название метода макс. правдоподобия.
. Отсюда и название метода макс. правдоподобия. .
.