
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Математическое ожидание случайной величины и его свойства.
Математическим ожиданием(средним значением)называют сумму следущегоряда,если он сходится М(х)= Св-ва М(х):1)М(с)=с:2)М(к*х)=к*М(х),к-постоянная величина,К=const Док-во:М(К*Х)= 3)Математическое ожидание M(x+-y)=M(x)+-M(y) M(x*y)=M(x)*M(y) M[x-M(x)]=0
Дисперсия и среднее квадратичное отклонение случайной величины и ее свойства. Опр:дисперсиейD(x) С.В.Х. называется математическое ожидание квадрата ее отклонение от математического ожидания D(x)=M[(x- Если С.В. дискретная с конечным числом значений,то D(x)= Если С.В.Х дискретная с бесконечно счетным,множествомзначений,тогда дисперсия D(x)= Опр:Среднимквадратическим отклонением Замечание:матем.ожидание М(х) характеризует среднее значение С.В. Дисперсия D(x)характеризует квадратичное отклонение С.В. от среднего значения: Св-ваD(x): 1)D(c)=0: 2)D(k*x)= Док-во:D(k*x)=M M 3)дисперсия D(x+-y)=D(x)+D(Y) 4)D(x)=M(x2)-(M(x))2 Док-во:D(x)=M(x-M(x))2)=M(x2-2x*M(x)+M2(x))=M(x2)-2M(x)*M(M(x))+M(M2(x))=M(x2)-2M(x)*M(x)+M2(x)=M(x2)-M2(x) M(x) M2(X)-постоянные величины
Математическое ожидание и дисперсия числа появления события в независимых опытах.
Пусть производится n независимых опытов, вероятность появления события в каждом из которых равна Р. Число появлений события в этих n опытах является случайной величиною Х распределённой по биномиальному закону. Однако, непосредственное вычисление её среднего значения громоздко. Для упрощения воспользуемся разложением, которым будем пользоваться в дальнейшем неоднократно: Число появления события в n опытах состоит изчисла появлений события в отдельных опытах, т.е. где 
Поэтому
или т.е. среднее число появлений события в n независимых опытах равно произведению числа опытов на вероятность появления события в одном опыте. Например, если вероятность попадания в цель при одном выстреле равна 0,1, то среднее число попадания в 20 выстрелах равно 20×0,1=2.
Производится n независимых испытаний и вероятность появления события в каждом испытании равна р. Выразим, как и прежде, число появления события Х через число появления события в отдельных опытах
Так как опыты независимы, то и связанные
Но каждая из случайных величин имеет закон распределения и где q=1-p В итоге имеем Среднее квадратическое отклонение числа появления событий в n независимых опытах равно
|
||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 316. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
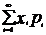
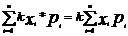
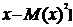
 ,где а= М(х)
,где а= М(х)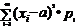 ,a=M(x),если ряд в правой части сходится
,a=M(x),если ряд в правой части сходится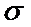 (х) С.В.Х. называется число
(х) С.В.Х. называется число 
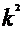 *D(x)
*D(x)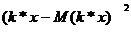 =
=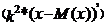 =
= 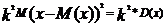

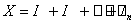
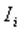 имеет закон распределения (принимает значение 1, если событие в данном опыте произошло, и значение 0, если событие в данном опыте не появилось).
имеет закон распределения (принимает значение 1, если событие в данном опыте произошло, и значение 0, если событие в данном опыте не появилось).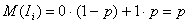

 с опытами случайные величины
с опытами случайные величины  независимы. А в силу независимости
независимы. А в силу независимости 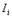 имеем
имеем
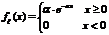
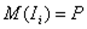 , поэтому по определению дисперсии
, поэтому по определению дисперсии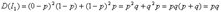 ,
,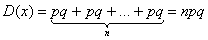 ,
, 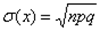
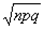 .
.