Система двух случайных величин. Ф-я распред, св-ва. Вероятн попадания в полуполосу и прямоугольник

Две сл. вел-ны могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми. Строгая функ-ная зав-ть реализуется редко, т.к. обе величины или одна из них подвержены еще действию случ.факторов, причем среди них могут быть и общие для обеих величин. В этом случае возникает статистическая зависимость. Стат-койнзвзав-ть, при к-рой изменение одной из величин влечет изменение распределения другой. В частности, стат.зав-тьпроявл.в том, что при изменении одной из величин изменяется среднее значение другой. В этом случае стат.зав-тьнзвкорреляционной

Определение 8.1. Функцией распределения F(x, y) двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y:

                        F( х, у ) = p ( X < x, Y < y ).                                                  

 Рис.1.

Это означает, что точка (X, Y) попадет в область, заштрихованную на рис. 1, если вершина прямого угла располагается в точке (х, у).

Замечание. Определение функции распределения справедливо как для непрерывной, так и для дискретной двумерной случайной величины

Свойства функции распределения.

0 ≤ F(x, y) ≤ 1 (так как F(x, y) является вероятностью).

F(x, y) есть неубывающая функция по каждому аргументу:

         F(x2, y) ≥ F(x1, y), если x2 > x1;

        F(x, y2) ≥ F(x, y1), если y2 > y1.

Доказательство. F(x2, y) = p(X < x2, Y < y) = p(X < x1, Y < y) + p(x1 ≤ X < x2, Y < y) ≥

≥ p(X < x1, Y < y) = F(x1, y). Аналогично доказывается и второе утверждение.

Имеют место предельные соотношения:

а) F(-∞, y) = 0; b) F(x, - ∞) = 0; c) F(- ∞, -∞) = 0; d) F( ∞, ∞) = 1.

Доказательство. События а), b) и с) невозможны ( так как невозможно событие Х<- ∞ или Y <- ∞), а событие d) достоверно, откуда следует справедливость приведенных равенств.

При у = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Х:

                                         F(x, ∞) = F1(x).

При х = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Y :

                                         F( ∞, y) = F2(y).

Доказательство. Так как событие Y < ∞ достоверно, то F(x, ∞) = р(Х < x) = F1(x). Аналогично доказывается второе утверждение.

27. Плотность распределения вероятностей двумерной случайной величины и её свойства. Плотностью совместного распределения вероятностей (двумерной плотностью вероятности)непрерывной двумерной случайной величины называется смешанная частная производная 2-го порядка от функции распределения:

.                                                        

Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами Δх и Δу к площади этого прямоугольника при

       Свойства двумерной плотности вероятности.

1) f(x, y) ≥ 0 (см. предыдущее замечание: вероятность попадания точки в прямоуголь-ник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен).

2)

(cледует из определения двумерной плотности вероятно-сти).

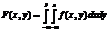
3)  (поскольку это вероятность того, что точка попадет на плос-кость Оху, то есть достоверного события).