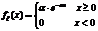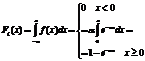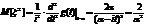Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Непрерывная случайная величина. Числовые характеристики непрерывных случайных величин.
Опр.: непрерывная СВ – это СВ имеющая бесконечное несчетное множество значений, покрывающая некоторый отрезок числовой оси. Опр.: Закон распределения СВ – это всякое соотношение устанавливающее связь между возможными значениями СВ и соответствующими ими вероятностями. Говорят, что СВ распределена по данному закону или подчинена этому закону распределения. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл
Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.
Средним квадратичным отклонениемназывается квадратный корень из дисперсии.
Закон равномерного распределения.
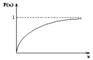
Непрерывная случайная величина имеет равномерноераспределение на отрезке [a,b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю. Для того, чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.
Экспоненциальный (показательный) закон распределения.
Вероятность попадания в заданный интервал. Правило трех сигм
вероятность попадания нормально распределенной случайной величины на заданный интервал:  Правилотрехсигм: Вероятность того, что нормальная случайная величина X отклоняется от своего математического ожидания а по модулю меньше, чем 3σ (три сигма), определяется формулой
.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 353. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

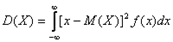
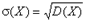
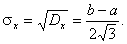
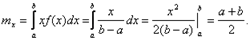
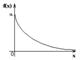 Случ вел-на ξ имеет экспоненц-ое (показательное) распр с параметром α>0, если имеет место след посл-ть распределения:
Случ вел-на ξ имеет экспоненц-ое (показательное) распр с параметром α>0, если имеет место след посл-ть распределения: