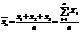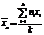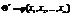Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Выборочная средняя и выборочная дисперсия.
Выборочная дисперсия Для того чтобы охарактизировать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения Выборочной средней 1) х1,х2,…,хn -все различны n-объём выборки
2) х1,х2,…,хk -появляются с опред.частотой. x1–появляется n1 раз x2 – n2 xk–nk
37&39&41. Точечная и интервальная оценки. Доверительный интервал.
Точечные оценки Точечной нзв оценку, к-рая опред-ся одним числом, например: генеральная средняя, выборочная средняя, групповая и общая средние, генеральная дисперсия, выборочная дисперсия и др.
xi – значения выборки При выборке малого объема точечная оценка может знач.отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.  Оценка неизвестного параметра называется интервальной, если она определяется 2 числами, концами интервала. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал (Ө1*;Ө 2*), относительно которого с заранее выбранной вероятностью γ можно утверждать, что внутри этого интервала находятся точные значения оцениваемого параметра. Интервал (Ө1*;Ө 2*), накрывающий с вероятностью γ истинное значение параметра Ө наз-ся доверительным интервалом. А вероятность γ наз-ся надежностью оценки или доверит. вероятностью. Часто дов. интервал выбирается симметрично относительно несмещенной точечной оценки Ө*, т.е. выбирается интервал вида (Ө*-ε; Ө*+ε) такой, что Р(|Ө-Ө*|<ε)=γ. Число ε>0 наз-ся точность оценки.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 281. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
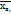 вводят сводную характеристику –выборочную дисперсию. Выборочной дисперсией
вводят сводную характеристику –выборочную дисперсию. Выборочной дисперсией 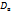 называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения
называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения 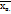 если все значения
если все значения 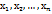 признака выборки объема nразличны, то
признака выборки объема nразличны, то 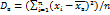 если же значения признака
если же значения признака 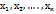 имеет соответственно частоты
имеет соответственно частоты 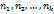 причем
причем 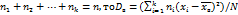 т.е. выборочная дисперсия есть средняя взвешаная квадратов отклонения с весами , равными соответствующим частотам. Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением. Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:
т.е. выборочная дисперсия есть средняя взвешаная квадратов отклонения с весами , равными соответствующим частотам. Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением. Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии: 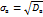
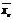 наз.среднее арифметическое значений признака выборочной совокупности.
наз.среднее арифметическое значений признака выборочной совокупности.