Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Закон распределения случайных величин входящих в системуДвумерной называют случайную величину (X, У), возможные значения которой есть пары чисел (х, у). Составляющие X и У, рассматриваемые одновременно, образуют систему двух случайных величин. Дискретной называют двумерную величину, составляющие которой дискретны. Законом распределениявероятностей двумерной случайной величины называют соответствие между возможными значениями и их вероятностями. Функцией распределения вероятностей двумерной случайной величины называют функцию F (х, у), определяющую для каждой пары чисел (х, у) вероятность того, что X примет значение, меньшее X, и при этом Y примет значение, меньшее у:
Рассмотрим случай двух дискретных случайных величин ( X,Y ). Считаем, что множество значений каждой из них конечно -
Сумма всех вероятностей , стоящих в матрице, равна единице как сумма вероятностей полной группы несовместных событий: Зная закон распределения системы ( Х,Y ), можно найти законы (ряды) распределения отдельных величин Х и Y, входящих в систему. Обозначим События несовместны, поэтому вероятность того, что Х примет значение В общем случае Т.е., для того, чтобы найти вероятность 
Если между случайными величинами Нормальное распределение. Функция Лапласа Нормальнымназывается распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.
Обозначим Тогда Т.к. интеграл Которая-называется функцией Лапласаили интегралом вероятностей. Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах. Ниже показан график функции Лапласа.
Функция Лапласа обладает следующими свойствами: 1) Ф(0) = 0;2) Ф(-х) = - Ф(х); 3) Ф(Y) = 1. Функцию Лапласа также называют функцией ошибок и обозначают erf x. Еще используется нормированнаяфункция Лапласа, которая связана с функцией Лапласа соотношением:
Ниже показан график нормированной функции Лапласа.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 329. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
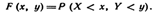
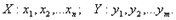 Обозначим
Обозначим - вероятность того, что Х примет значение
- вероятность того, что Х примет значение 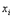 ,а Y – значение
,а Y – значение 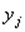 . Законом распределения системы ( X,Y ) называется совокупность всех возможных значений , т.е. пар чисел
. Законом распределения системы ( X,Y ) называется совокупность всех возможных значений , т.е. пар чисел 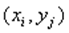 и соответствующих им вероятностей
и соответствующих им вероятностей  . Обычно закон распределения задается в виде прямоугольнойтаблицы с двойным входом:
. Обычно закон распределения задается в виде прямоугольнойтаблицы с двойным входом: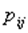
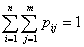
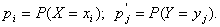

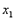 по теореме сложения вероятностей
по теореме сложения вероятностей 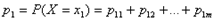 , т.е. равна сумме вероятностей «столбца
, т.е. равна сумме вероятностей «столбца 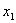 » .
» .
 и, аналогично,
и, аналогично, 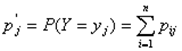 .
.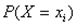
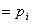 , надо просуммировать вероятности «столбца
, надо просуммировать вероятности «столбца 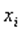 ». Аналогично, сложив вероятности «строки
». Аналогично, сложив вероятности «строки 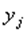 », получим вероятность
», получим вероятность 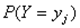
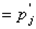 . После этого можно составлять законы распределения для Х и Y.
. После этого можно составлять законы распределения для Х и Y.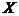 и
и  существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация
существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация  .
.

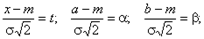
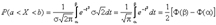
 не выражается через элементарные функции, то вводится в рассмотрение функция
не выражается через элементарные функции, то вводится в рассмотрение функция