
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Статистическое распределение выборки.Эмпирическая функция распределения
Выборка- множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании. Cтатистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант хi и соответствующих им частот ni или относительных частот wi. Статистическое распределение выборки удобно представлять в форме таблицы распределения частот, называемой статистическим дискретным рядом распределения.
Эмпирической функцией распределения называют функцию F*(x), определяющую для каждого значения x относительную частоту события X<x. По определению:
Где Свойства эмпирической функции распределения: 1) Значение эмпирической функции принадлежат отрезку [0;1] 2) F*(x)- неубывающая функция 3) если
Полигон и гистограмма.
Основные графики вариационного ряда: полигон и гистограмма. Полигономчастот называют ломаную, отрезки которой соединяют точки Для построения полигона частот на оси абсцисс откладывают варианты х2, а на оси ординат – соответствующие им частоты ni. Точки (хi,ni) соединяют отрезками и получают полигон частот. Гистограммойчастот называют ступенчатую фигуру, состоящую из прямоугольников, одна из сторон которых - частичные интервалы с длиною h, другая- отношение (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h. Площадь i-го частичного прямоугольника равна h•ni/h=ni - сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки. 
36. Статистические оценки параметров распределения.
Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Несмещённой называют статистическую оценку Ө*, математическое ожидание которой равно оцениваемому параметру Ө при любом объёме выборки, т.е. M(Ө*)= Ө Смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру. Эффективной называют статистическую оценку, которая (при заданном объёме выборки n) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объёма (n велико!) к статистическим оценкам предъявляется требование состоятельности. Состоятельной называют статистическую оценку, которая при n →∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещённой оценки при n→∞ стремится к нулю, то такая оценка оказывается и состоятельной.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 322. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 - число вариант, меньших x; x- объём выборки.
- число вариант, меньших x; x- объём выборки. - наименьшая варианта, то F*(x)=0 при x≤
- наименьшая варианта, то F*(x)=0 при x≤ 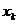 - наибольшая варианта, то F*(x)=1 при x>
- наибольшая варианта, то F*(x)=1 при x>  .
.