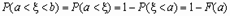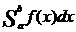Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дискретные случайные события и возможности их описания.Опр.: СВ- это переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений. (Примеры: число бракованных изделий в данной партии, расход электроэнергии предприятия) Опр.: ДСВ – это СВ с конечным или бесконечным, но счетным множеством её значений (см.выше 1-ый пример) Для случайных величин (далее - СВ) приходится использовать особые, статистические методы их описания. Дискретное описание заключается в том, что указываются все возможные значения данной величины (например - 7 цветов обычного спектра) и для каждой из них указывается вероятность или частота наблюдений именного этого значения при бесконечно большом числе всех наблюдений. Доказанно, что при увеличении числа наблюдений в определенных условиях за значениями некоторой дискретной величины частота повторений данного значения будет все больше приближаться к некоторому фиксированному значению - которое и есть вероятность этого значения.
Закон распределения дискретной случайной величины. Многоугольник распределения. Опр.: Закон распределения СВ – это всякое соотношение устанавливающее связь между возможными значениями СВ и соответствующими ими вероятностями. Говорят, что СВ распределена по данному закону или подчинена этому закону распределения. ЗАКОН распределения ДСВ может быть задан в виде таблицы:
Х: - ряд распределения ДСВ где, х1, х2,…, хn– возможные значения СВ, в порядке возрастания p1, p2,..., pn– соответствующие им вероятности. Очевидно, что суммы вероятностей pi=1
Т.к.события Х=х, х=1,…,х= хn образуют полную группу событий.  Закон распределения дискретной случайной величины может быть представлен в виде многоугольника распределения – фигуры, состоящей из точек, соединенных отрезками
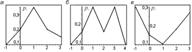
Многоугольники унимодального (а), полимодального (б) и антимодального (в) распределений.
Функция распределения и ее свойства. Вероятность попадания случайной величины на заданный интервал.
Опр.: ф-я распределения С.В.Х. называется ф-я F(x)выражающая для каждого Х вероятность того,что примет значение:F(x)=P(x<x) Ф-я F(x) называется интегральная ф-я распределения. Св-ва ф-ииF(x): 1)0<=F(x)<=1;2)F(x)-неубыв.ф-я на всей числовой оси.; 3) График:составим ф-ю распределения F(z)=? 1)z<=-1следовательно F(z)=P(z<z)=0 2)-1<z<=0след-ноF(z)=P(z<z)=P(z=-1)=0,08; 3)0<z<=1cлед.F(z)=P(z<z)=P(z=-1)+P(z=0)=0,34 4)1<z<=2 F(z)=p(Z<z)=P(Z=-1)+P(Z=0)+ P(Z=1)=0,08+0,26+0,22=0,56
0,08;-1<z<=0 F(X)= 0,34;0<z<1 0,56;1<z<=2 0,76;2<z<=3 0,96;3<z<=4 1;z>4
Вероятность того, что значение дискретной случайной величины Fx (x) попадает в интервал (a, b), равнаяP(a < x < b) = Fx (b) -Fx (a), вычисляется по формулам: Если a= - если b= , то .
Плотность распределения и ее свойства. Вероятностный и геометрический смысл плотности распределения.
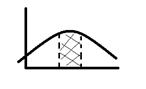
Плотностью распределения вероятностей непрерывной С.В. называют первую производную от ф-ии распределения:f(x)=F(x) Св-ва:1)плотность распределения неотриц.,т.е.f(x)>=0 2)вер-ть попадания непрерывнрой С.В. в интервал(а,в)равна интервалу от ее плотности вероятности в пределах от а до в P(a<x<b)= Геометрически,полученная вероятность равна S фигуры ограниченной сверху кривой распределения и опирается на отрезок ав
|
|||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 327. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
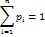
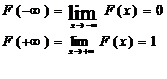 4)P(x1<=x<=x2)=F(x2)-F(x1)
4)P(x1<=x<=x2)=F(x2)-F(x1)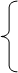
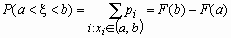
 , то
, то 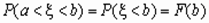 ,
,