
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формула полной вероятности.Опр.: пусть событие А может произойти только совместно с одним из событий Н1, Н2,…,Нn образующих полную группу несовместных событий, тогда соб. Н1, Н2,…,Нnназываются гипотезами. Теорема: вероятность соб.А наступающего совместно с гипотезами Н1, Н2,…,Нnравна:
где, Р(Нi) – вероятность i-той гипотезы РНi(А) – вероятность соб.А при условии реализации гипотезы Нi Доказательство: соб.А можно считать суммой попарно несовместных событий АН1, АН2, …АНn несовместные события, тогда из теорем сложения вероятностей: Р(А)+Р(АН1+…+ АНn)=Р(АН1)+…+Р(АНn)= =РНi(А)* Р(Н1)+…+ РНn(А)* Р(Нn)=
9. Формула Бейеса. Теорема гипотез (формула Байеса)– следствие теоремы умножения и ф-лы полной вероятности. Имеется группа несовместных гипотез H1,H2...Hn, чьи вероятности равны соответственно P(H1),P(H2)...P(Hn). В рез. Σ происходит событие А. Как следует изменить вероятности гипотез в связи с появлением А (найти условную вероятность P(Hi|A))? Выражая P(A) из ф-лы полной вероятности, имеем соотношение Байеса:
Формула Бернулли. Пусть производится серия из n независимых испытаний и в каждом испытании событие А наступает с одной и той же вероятностью P(A)=p и не наступает с вероятностью  Доказательство: Рассмотрим серию из n испытаний, в которых событие А произошло m раз:
Формула Пуассона и условия ее применимости.
Использование формулы Бернулли при больших n и m вызывает трудности из-за громоздких вычислений => возникает необходимость в отыскании вероятности Теорема: если число испытаний неограниченно увеличивается n
Доказательство: λ=np =>p=λ/n подставляем это равенство в формулу:
Перейдем к пределу в обеих частях неравенства при n
Формулу Пуассона применяют обычно когда n≥50, np≤10
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 332. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 - формула полной вероятности
- формула полной вероятности
 .Док-во: вероятность появления А опред. по ф-ле полной вероятности:
.Док-во: вероятность появления А опред. по ф-ле полной вероятности:  . Поищем условные вероятности
. Поищем условные вероятности  при условии, что произошло событие А. По теореме умножения имеем
при условии, что произошло событие А. По теореме умножения имеем  . Подставим P(A), получим
. Подставим P(A), получим 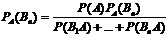 . чтд. Ф-лы Байеса позволяют переоценить вероятности после того, как становится известным результат испытания, в итоге которого появилось событие А.
. чтд. Ф-лы Байеса позволяют переоценить вероятности после того, как становится известным результат испытания, в итоге которого появилось событие А.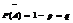 . Условно появление события А называется «успехом», а не появление - «неудачей». Испытания называются независимыми, если исход каждого последующего не зависит от исходов предыдущих испытаний. Последовательность независимых испытаний такого рода называется схемой Бернулли. Вероятность того, что в n независимых испытаниях событие А произойдет ровно m раз – Pn(m). Тогда имеет место формула Бернулли: Pn (m)=
. Условно появление события А называется «успехом», а не появление - «неудачей». Испытания называются независимыми, если исход каждого последующего не зависит от исходов предыдущих испытаний. Последовательность независимых испытаний такого рода называется схемой Бернулли. Вероятность того, что в n независимых испытаниях событие А произойдет ровно m раз – Pn(m). Тогда имеет место формула Бернулли: Pn (m)=  .
. .Вычислим вероятность этого произведения: P (
.Вычислим вероятность этого произведения: P (  =
=  =pmqn – m. Pn (m)=
=pmqn – m. Pn (m)=  обеспечивающих необходимую точность.
обеспечивающих необходимую точность. и вероятность р наступления соб.А в каждом испытании уменьшается р
и вероятность р наступления соб.А в каждом испытании уменьшается р  , но так что их произведение n*p остается величиной постоянной (λ=np=const), то вероятность
, но так что их произведение n*p остается величиной постоянной (λ=np=const), то вероятность 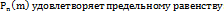


 =
=  =
=  =
= 

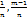 ,
, 
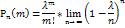
 =>
=> 