
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Зависимые и независимые события. Теорема умножения вероятностей.Опр.: условной вероятностью Теорема (умножения зависимых событий): вероятность произведения двух событий равна произведению вероятности одного события на условную вероятность другого, при условии, что 1-ое событие произошло: Доказательство: Пусть n-число возможных исходов опыта; mА-число исходов благоприятствующих соб.А; mB-//-соб.В, mАВ – число исходов опыта, при котором происходят оба события,. для вычисления условной вероятности
=> Пример: для поражения цели необходимо попасть в неё дважды. Вероятность 1-го попадания 0,2, затем она не меняется при промахах, но после 1-го попадания увеличивается в 2 раза. Найти вероятность того что цель будет поражена первыми двумя выстрелами. Решение: соб.А – попадания при первом выстреле Соб.В - //- при 2-ом выстреле
А и В совместные события
Пусть вероятность соб.В не зависит от появления соб.А Событие В называют независимым от события А, если появление соб.А не изменяет вероятности события В, т.е. если условная вероятность соб.В равна его безусловной вероятности: 
т.е.условная вероятность соб.А в предположении, что наступило соб.В, равна его безусловной вероятности. Другими словами, соб.А не зависит от соб.В Итак, если соб.В не зависит от соб.А, то и соб.А не зависит от соб.В; это значит, что свойство независимости событий взаимно. Для независимых событий теорема умножения
Т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий. Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми. На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий, поэтому событие «первое орудие поразило цель» и «второе орудие поразило цель» независимы.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 330. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
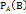 соб.А называется вероятность соб.В при условии, что событие А произошло (пример: пусть соб.А - это извлечение из колоды в 32 карты туза; соб.В – вторая вынутая карта из колоды оказалось тузом. Если после 1-го раза карта возвращается в колоду, то вероятность вынуть туз не меняется и равна 4/32, если же 1-я карта в колоду не возвращается, то осуществление соб.А прибудет к тому, что в колоде остается 31 карта из которой 3 туза
соб.А называется вероятность соб.В при условии, что событие А произошло (пример: пусть соб.А - это извлечение из колоды в 32 карты туза; соб.В – вторая вынутая карта из колоды оказалось тузом. Если после 1-го раза карта возвращается в колоду, то вероятность вынуть туз не меняется и равна 4/32, если же 1-я карта в колоду не возвращается, то осуществление соб.А прибудет к тому, что в колоде остается 31 карта из которой 3 туза 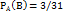 – условная вероятность
– условная вероятность
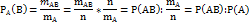
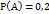 ,
, 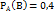
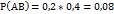
 подставив данное равенство в
подставив данное равенство в получим
получим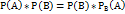 , отсюда
, отсюда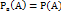 ,
,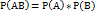 ,
,