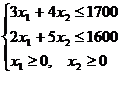Свойства решений задач линейного программирования

1. Допустимое множество задачи ЛП либо пусто, либо является выпуклым многогранником в Rn (как пересечение полупространств, описываемых неравенствами (2)-(3)). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.

2. Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации - ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.

3. Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечное множество точек максимума или минимума).

Методами решения задач ЛП являются:

1. графический метод (в случае двух переменных),

2. симплекс-метод или его разновидности (в общем случае).

Двумерные задачи линейного программирования. Графический метод решения. Исследование на разрешимость

Двумерная задача линейного программирования - задача линейного программирования, количество переменных которой равно 2.

Переменные принято обозначать х₁ и х₂. Рассмотренная ранее задача линейного программирования является двумерной.

В общем виде двумерную задачу линейного программирования можно представить в следующем образом.

Определить значение переменных х₁ и х₂, при которых линейная целевая функция F достигает максимум (минимум)

F=с₁x₁ + с₂х₂ → max (min)

Среди ограничений могут одновременно встречаться знаки ≥, ≤ и =. Коэффициенты a_ij, b_i, c_j, i = l..m, j =1,2 любые действительные числа (возможно и 0).

Двумерные задачи линейного программирования обычно решаются графически.

Пример 1.Решим полученную двумерную задачу линейного программирования графически.

F=2x₁ + 4х₂ → max

Решение