
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Построение потока в сети с двойным ограничением потока по дугамВ данной задаче наряду с рассмотренными условиями выполняется ещё одно дополнительное условие:
Очевидно, что в данной ситуации уменьшение потока на обратных дугах будет ограничено нижней границей Упражнения a) Определить допустимый поток в данной модифицированной сети и привести формулировку задачи о нахождении максимального потока. Сформулировать условия существования допустимого потока. b) Модифицировать алгоритм Форда-Фалкерсона для построения максимального потока в сети с двойным ограничением потока по дугам.
Построение потока в сети с пропускными способностями узлов Такой сетью является сеть, в которой узлы (вершины) могут также обладать пропускной способностью, т.е. когда дополнительно заданы числа c(x) для некоторых Упражнения a) Определить допустимый поток в данной модифицированной сети и привести формулировку задачи о нахождении максимального потока. b) Модифицировать алгоритм Форда-Фалкерсона Для построения максимального потока в сети с пропускными способностями узлов.
Построение потока в сети с несколькими источниками-стоками Данная модификация предполагает, что в сети заданы n источников s1, s2, …, sn и m стоков t1, t2, …, tm. Чтобы свести данную задачу к базовой, вводят в рассмотрение фиктивные источники – главный источник S и главный сток T, а также фиктивные дуги (S, s1), …, (S, sn) и (t1, T), …, (tm, T) и полагают пропускную способность дуг, выходящих из S и соответственно входящих в T, равной 
Построение потока в сети с неориентированными ребрами В данной модификации предполагается, что в сети имеются ребра, т.е. дуги без заданной ориентации, но с заданными пропускными способностями. Для приведения данной сети к базовой каждое ребро заменяется на две дуги противоположной ориентации, но с теми же вершинами и пропускной способностью, равной пропускной способности ребра. Упражнения a) Определить допустимый поток в данной модифицированной сети и привести формулировку задачи о нахождении максимального потока. b) Модифицировать алгоритм Форда-Фалкерсона для построения максимального потока в сети с неориентированными ребрами.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 444. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
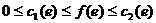 для любой дуги
для любой дуги  .
.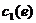 для потока на рассматриваемой дуге.
для потока на рассматриваемой дуге.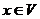 . Для того, чтобы свести данную задачу к базовой, необходимо представить, что каждая вершина x, обладающая пропускной способностью, «растягивается» в дополнительную дугу (x1, x2), которой присваивается пропускная способность вершины x, т.е.
. Для того, чтобы свести данную задачу к базовой, необходимо представить, что каждая вершина x, обладающая пропускной способностью, «растягивается» в дополнительную дугу (x1, x2), которой присваивается пропускная способность вершины x, т.е.  .
. .
.