
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Примеры решения задач симплекс-методомПример 1. (задача об оптимальном распределении материалов). Имеющийся фонд материалов Таблица 4.3
Решение Математическая модель задачи
Введя дополнительные переменные х6, х7 и х8, получим ее каноническую форму:
По индексной строке видно, что начальный опорный план неоптимален. Так как дополнительные переменные в канонической форме составляют допустимый единичный базис, то условия задачи заносим в симплексную таблицу. Таблица 4.4
Разрешающие элементы выбираем по описанным выше правилам. Все вычисления выполняются согласно правилам симплексных преобразований.  На втором шаге преобразований получаем оптимальный план – все оценки положительны. Итак, х0 = (0; 15 952; 0; 9286; 0; 14 286; 0; 0), т. е. имеющиеся материалы нужно распределить на выпуск продукции П2 в объеме х*2 = 15 952 ед. и П4 в объеме х*4 = 9286 ед. Реализация этой продукции даст 195 238 ден. ед. На выпуск 15 952 ед. продукции П2 нужно выделить: первого материала 0,9 × 15 952 = 14 356,8 ед., второго материала 0,3 ×15 952 = 4785 ед., третьего материала 2,1 × 15 952 = 33 499,1 ед. На выпуск 9286 ед. продукции П4 нужно выделить: первого материала 2,3 × 9286 = 21 357,8 ед., второго материала 2,5 × 9286 = 23 215 ед., третьего материала 0,7 × 9286 = 6500,2 ед. Дополнительные переменные в оптимальном плане показывают объем неиспользуемых материалов: первого материала остается 14 286,4 ед., второй и третий материалы используются полностью. Пример 2. Используя искусственный базис, решить ЗЛП
РешениеСоставляем соответствующую М – задачу и решаем ее обычным способом. После второй итерации все оценки(см. табл.) неположительны: Dj £ 0 ( Таблица 4.5
Теория двойственности в линейном программировании |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 480. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 нужно так распределить между изготовителями, чтобы получить максимальную прибыль от реализации всей продукции, произведенной из данных материалов. Нормы
нужно так распределить между изготовителями, чтобы получить максимальную прибыль от реализации всей продукции, произведенной из данных материалов. Нормы 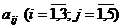 расхода на единицу продукции и прибыль сj, получаемая от реализованной единицы продукции, представлены в табл.
расхода на единицу продукции и прибыль сj, получаемая от реализованной единицы продукции, представлены в табл.

 2,5
2,5

 ). Следовательно, по признаку оптимальности опорный план (0; 0; 3; 0; 0; 3) оптимален. Но так как в оптимальном плане искусственная переменная w не равна нулю, то система ограничений исходной задачи несовместна. Задача решения не имеет.
). Следовательно, по признаку оптимальности опорный план (0; 0; 3; 0; 0; 3) оптимален. Но так как в оптимальном плане искусственная переменная w не равна нулю, то система ограничений исходной задачи несовместна. Задача решения не имеет.