
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Модификация алгоритма Флойда
Шаг 0. Пусть N = {1, 2, …n}- множество узлов сети. На j-й итерации работы алгоритма будем строить матрицу длин Алгоритм начинает работу с матрицей Шаг 1. Пусть матрицы Шаг 2. Построим матрицы
Если Если
Шаг 3. Элемент матрицы
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 396. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
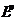 , элемент которой
, элемент которой  равен длине «узкого» места (i, j) – цепи, промежуточными узлами в которой могут быть лишь узлы из множества {1, 2,…, p}; и справочную матрицу
равен длине «узкого» места (i, j) – цепи, промежуточными узлами в которой могут быть лишь узлы из множества {1, 2,…, p}; и справочную матрицу  , каждый элемент
, каждый элемент 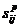 которой указывает первый после узла i узел в такой сети.
которой указывает первый после узла i узел в такой сети. , где
, где  , если меняется дуга из i в j (в противном случае
, если меняется дуга из i в j (в противном случае 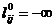 ), и с матрицей
), и с матрицей  После построения матриц
После построения матриц  и
и  для каждого p=1, 2, …, n, используя для вычислений элементы матриц, полученных на предыдущих итерациях, необходимо выполнить следующую процедуру:
для каждого p=1, 2, …, n, используя для вычислений элементы матриц, полученных на предыдущих итерациях, необходимо выполнить следующую процедуру: и
и  найдены. Выделим элементы p-й строки и p-го столбца матрицы
найдены. Выделим элементы p-й строки и p-го столбца матрицы  . Назовем эти множества элементов базовой строкой и базовым столбцом соответственно.
. Назовем эти множества элементов базовой строкой и базовым столбцом соответственно. и
и  , исходя из следующего правила: для
, исходя из следующего правила: для 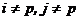
 , то
, то  и
и  .
.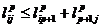 , то
, то  и
и  .
. равен «узкому» месту в цепи из узла i в узел j. Элемент
равен «узкому» месту в цепи из узла i в узел j. Элемент 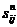 есть узел, стоящий после узла i в этой цепи.
есть узел, стоящий после узла i в этой цепи.