
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчет и анализ сетевых моделейКалендарное планирование предусматривает определение моментов начала и окончания каждой работы и других временных характеристик сетевого графика. Это позволяет проанализировать сетевую модель, выявить критические работы, непосредственно определяющие срок выполнения проекта, провести оптимизацию использования ресурсов (временных, финансовых, исполнителей). Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика (рис.8.1): 1. 2. 3.
Рис.2.7. Отображение временных параметров событий на сетевом графике Ранние сроки свершения событий 1) для исходного события И 2) для всех остальных событий I
где максимум берется по всем работам
Рис.2.8. Расчет раннего срока Поздние сроки свершения событий 1) для завершающего события З 2) для всех остальных событий
где минимум берется по всем работам
Рис.2.9. Расчет позднего срока  Временные параметры работ определяются на основе ранних и поздних сроков событий: § § § § § § Путь – это последовательность работ в сетевом графике (в частном случае это одна работа), в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы. Полный путь – это путь от исходного до завершающего события. Критический путь – максимальный по продолжительности полный путь. Работы, лежащие на критическом пути, называют критическими. Критические работы имеют нулевые свободные и полные резервы. Подкритический путь – полный путь, ближайший по длительности к критическому пути. Для проведения анализа временных параметров сетевой модели используют график привязки, который отображает взаимосвязь выполняемых работ во времени. По вертикальной оси графика привязки откладываются коды работ, по горизонтальной оси – отрезки, соответствующие длительностям работ (раннее начало и раннее окончание работ). График привязки можно построить на основе данных о продолжительности работ. При этом необходимо помнить, что работа Задача №1 Компания разрабатывает строительный проект. Исходные данные по основным операциям проекта представлены в табл.2.1. Постройте сетевую модель проекта, определите критические пути модели и проанализируйте, как влияет на ход выполнения проекта задержка работы D на 4 недели. Таблица 2.1 Исходные данные
Решение: Построим сетевую модель и рассчитаем временные параметры событий (рис.8.3). При поиске критических путей на сетевом графике будем использовать следующие условия его критичности: § необходимое условие – нулевые резервы событий, лежащих на критическом пути; § достаточное условие – нулевые полные резервы работ, лежащих на критическом пути. Согласно необходимому условию два полных пути сетевой модели (см. рис.3)
Путь Таким образом, сетевая модель имеет единственный критический путь
Рис.2.10. Сетевой график
Задача №2 По данным о кодах и длительностях работ в днях (табл.2.2) постройте график привязки сетевой модели, определите критические пути и их длительность. Определите свободные и полные резервы каждой работы, отметьте на графике привязки свободные резервы работ. Таблица 2.2 Исходные данные задачи №2
Общие рекомендации При поиске критических путей следует помнить, что признаком критической работы являются нулевые значения резервов времени. Это означает, что каждая последующая критическая работа будет начинаться строго в момент окончания предыдущей критической работы. Вследствие этого сдвиг любой из работ критического пути обязательно приведет к увеличению первоначальной длительности проекта ( Из вышеприведенных соображений следует способ определения критического пути на графике привязки (все найденные работы выписываются последовательно справа налево): 1) найти на графике привязки и выписать работу (i,j), которая заканчивается позже всех остальных. Это будет последняя работа критического пути (ее конечное событие иметь номер завершающего события сети); 2) из всех работ сети (k,i), конечное событие которых i совпадает с начальным событием i работы (i,j), найденной в п.1), выбрать и выписать ту, которая на графике вплотную примыкает к работе (i,j); 3) из всех работ сети (l,k), конечное событие которых k совпадает с начальным событием k работы (k,i), найденной в п.2), выбрать и выписать ту, которая на графике вплотную примыкает к работе (k,i); 4) продолжать п.3) до тех пор, пока не будет найдена исходная работа сети, т.е. начинающаяся в нулевой момент времени (ее начальное событие будет иметь номер исходного события сети, например, 1). Следует заметить, что если в сетевой модели несколько критических путей, то, выполняя вышеописанные действия, можно обнаружить несколько работ, удовлетворяющих сформулированным требованиям. В таком случае необходимо продолжать поиск по каждой из таких работ в отдельности. В сложных сетевых моделях подобные разветвления могут привести к большим затратам времени на поиск критически путей. Тем не менее, такой способ хорош для учебных целей, поскольку дает понимание значения критических работ в сетевой модели и учит "читать" и понимать график привязки. Решение: I. Поиск критических путей 1) Построим график привязки (рис.2.11).
Рис.2.11 График привязки задачи №2 2) Начнем поиск критических путей (справа налево) с работ, завершающих проект. На графике привязки (см. рис.2.11) две работы (6,7) и (3,7), которые заканчиваются позже остальных в завершающем событии №7. Записываем работы, определенные как критические справа налево (2.1)
3) Найдем критическую работу из
(2.2) 4) Найдем критическую работу из
(2.3) 5) Найдем критическую работу из
6) Аналогичный поиск работ критического пути В другой форме записи 7) Для наглядности выделим на графике привязки критические работы жирной линией. II. Поиск резервов работ 1) Для всех найденных критических работ впишем в табл.3 нулевые значения свободного и полного резервов. Рассмотрим некритические работы, начиная с конца табл.2.3. Таблица 2.3 Резервы работ из задачи №2
2) Работа (5,7), согласно графику привязки (см. рис.2.4) заканчивается в 13-й день, а завершающее событие 7 сети, в которое она входит, наступает лишь в 14-й день. Т.е. если работа (5,7) задержится на 1 день, то это не повлияет на срок выполнения проекта ( 3) Работа (4,6) заканчивается в 8-й день, в то время как последующая работа (6,7) начинается в 10-й день. То есть, работа (4,6) может задержаться на 2 дня и это никак не повлияет на время начала последующей работы (6,7), т.е. Правило №2.1 Полный резерв любой работы складывается из собственного свободного резерва и минимального из полных резервов непосредственно следующих работ. За работой (4,6) следует только критическая работа (6,7) с нулевым полным резервом. Поэтому 4) Работа (4,5) заканчивается в 12-й день, в этот же день начинается следующая работа (5,7), т.е. любая задержка выполнения работы (4,5) приведет к задержке начала работы (5,7). Это означает, что работа (4,5) не имеет свободного резерва
5) Работа (1,5) заканчивается в 10-й день, в то время как последующая работа (5,7) начинается в 12-й день. Т.е. работа (1,5) может задержаться на 2 дня и это никак не повлияет на время начала последующей работы (5,7), т.е.
6) Работа (1,4) заканчивается во 2-й день, и в этот же день начинаются следущие работы (4,5) и (4,6). Т.е. работа (1,4) не имеет свободного резерва времени
7) Работа (1,3) заканчивается в 3-й день, а следующие за ней работы (3,6) и (3,7) начинаются в 5-й день, т.е. 8) Ненулевые свободные резервы работ обозначены на графике привязки фигурными скобками (см. рис.2.11).
Линейное программирование Примеры задач ЛП Линейное программирование - это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием. Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы. Математическая модель любой задачи линейного программирования включает в себя: 1) максимум или минимум целевой функции (критерий оптимальности); 2) систему ограничений в форме линейных уравнений и неравенств; 3) требование неотрицательности переменных. Рассмотрим алгоритм составления математической модели задачи на примере. Пример 1.Фирма производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3 м2 досок, а для модели В - 4 м2. Фирма может получать от своих поставщиков до 1700 м2 досок в неделю. Для каждого изделия модели А требуется 12 мин. машинного времени, а для изделия модели В - 30 мин. В неделю можно использовать 160 часов машинного времени. Сколько изделий каждой модели следует выпускать фирме в неделю, если каждое изделие модели А приносит 2 дол. прибыли, а каждое изделие модели В - 4 дол. прибыли? Сведем все данные в табл. Таблица 3.1
Построение математической модели. Пусть х1 - количество выпущенных за неделю полок модели А, х2 - количество выпущенных полок модели В. Тогда: 3x1 - количество досок требуемых на неделю для изготовления полок модели А, 4х2- количество досок требуемых на неделю для изготовления полок модели В. 3x1 + 4х2 - количество досок требуемых на неделю для изготовления книжных полок двух моделей, а по условию задачи это число не должно превышать 1700 м2. Следовательно, получаем первое ограничение: 3x1 + 4х2 ≤ 1700 (1) Найдем ограничение на использование машинного времени: 12 мин. составляют 0,2 часа, а 30 мин. - 0,5 часа. Таким образом: 0,2x1 - количество времени, требуемое на неделю для обработки полок модели А; 0,5х2 - количество времени, требуемое на неделю для обработки полок модели В; 0,2x1 + 0,5х2 - количество времени, требуемое на неделю для обработки двух моделей, а по условию задачи это число не должно превышать 160 часов. Следовательно, получаем второе ограничение: 0,2x1 + 0,5х2 ≤ 160 или 2x1 + 5х2 ≤ 1600 (2) Кроме того, поскольку x1 и х2 выражают еженедельный объем выпускаемых изделий, то они не могут быть отрицательными, то есть x1 ≥ 0, х2 ≥0 (3) Наша задача состоит в том, чтобы найти такие значения x1 и х2, при которых еженедельная прибыль будет максимальной. Составим выражение для еженедельной прибыли: 2x1 - еженедельная прибыль, получаемая от продажи полок модели А. 4х2 - еженедельная прибыль, получаемая от продажи полок модели В. F=2x1 + 4х2 - еженедельная прибыль, которая должна быть максимальной. Таким образом, имеем следующую математическую модель для данной задачи. F=2x1 + 4х2 → max
Полученная модель является задачей линейного программирования. Функция F это целевая функция, она является линейной функцией своих переменных (x1, х2). Ограничения на эти переменные (1) и (2) тоже являются линейными. Выполнено условие неотрицательности для переменных x1 и х2. Необходимо найти значения переменных x1 и х2, при которых данная функция F принимает максимальное значение, при соблюдении ограничений, накладываемых на эти переменные. Решения, удовлетворяющие системе ограничений и требованием неотрицательности, являются допустимыми, а решения, удовлетворяющие одновременно и требованием минимизации (максимизации) функции в целом являются оптимальными. Задача математического программирования называется задачей линейного программирования, если целевая функция f есть линейная функция, а множество допустимых решений х задается с помощью линейных неравенств или линейных уравнений. В общем виде задачу линейного программирования можно представить в следующем образом.
(l)-(3) - это стандартная постановка задачи ЛП (в общем случае в ограничениях (2) могут быть различные соотношения вида «≤», «≥», «=»). с1,…, cn - коэффициенты при целевой функции, а11, …, аkn - коэффициенты при ограничениях, b1, …, bk - свободные члены при ограничениях. Все они являются известными числами (заданы). Неизвестными являются переменные х1, …, хn. В задачах (1) - (3) требуется найти такие значения переменных 1. эти переменные удовлетворяли всем ограничениям (2) и (3) (условие допустимости); 2. В точке х* = ( Аналогично ставится задача на минимум. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 397. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 – ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
– ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i; – поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
– поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети; – резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения проекта в целом.
– резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения проекта в целом.
 ;
;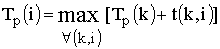 ,
, , входящим в событие i;
, входящим в событие i;  – длительность работы (k,i) (рис.2.8).
– длительность работы (k,i) (рис.2.8).
 ;
; ,
,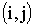 , выходящим из события i;
, выходящим из события i;  – длительность работы (k,i) (рис.2.9).
– длительность работы (k,i) (рис.2.9).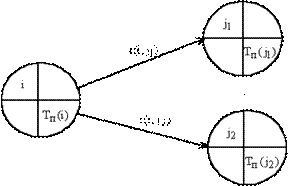
 – ранний срок начала работы;
– ранний срок начала работы; – ранний срок окончания работы;
– ранний срок окончания работы; – поздний срок окончания работы;
– поздний срок окончания работы; – поздний срок начала работы;
– поздний срок начала работы;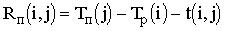 – полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы
– полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы 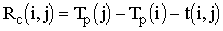 – свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы
– свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы  может выполняться только после того как будут выполнены все предшествующие ей работы
может выполняться только после того как будут выполнены все предшествующие ей работы  .
. и
и  могут быть критическими. Проверим достаточное условие критичности для работ (1,2) и (1,3)
могут быть критическими. Проверим достаточное условие критичности для работ (1,2) и (1,3)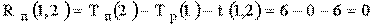 ;
;
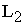 , начинающийся с работы (1,3) не является критическим, т.к. как минимум одна из его работ (1,3,) не является критической. Работа (1,3) имеет ненулевой полный резерв, а значит может быть задержана с выполнением, что недопустимо для критических работ.
, начинающийся с работы (1,3) не является критическим, т.к. как минимум одна из его работ (1,3,) не является критической. Работа (1,3) имеет ненулевой полный резерв, а значит может быть задержана с выполнением, что недопустимо для критических работ. длительностью
длительностью  недель. За выполнением работ этого пути необходим особый контроль, т.к. любое увеличение их длительности нарушит срок выполнения проекта в целом.
недель. За выполнением работ этого пути необходим особый контроль, т.к. любое увеличение их длительности нарушит срок выполнения проекта в целом. Работа D или (2,5) не является критической, ее полный резерв равен 3-м неделям. Это означает, что при задержке работы в пределах 3-х недель срок выполнения проекта не будет нарушен. Поэтому если согласно условию работа D задержится на 4 недели, то весь проект закончится на 1 неделю позже.
Работа D или (2,5) не является критической, ее полный резерв равен 3-м неделям. Это означает, что при задержке работы в пределах 3-х недель срок выполнения проекта не будет нарушен. Поэтому если согласно условию работа D задержится на 4 недели, то весь проект закончится на 1 неделю позже. ). Кроме того, следует учесть, что критический путь является полным, т.е. соединяет исходное и завершающее события сети. Поэтому на графике привязки первая из работ критического пути всегда начинается в исходном событии сети с нулевого (начального) момента времени, а последняя из работ критического пути всегда завершается позже всех остальных работ сети в завершающем событии.
). Кроме того, следует учесть, что критический путь является полным, т.е. соединяет исходное и завершающее события сети. Поэтому на графике привязки первая из работ критического пути всегда начинается в исходном событии сети с нулевого (начального) момента времени, а последняя из работ критического пути всегда завершается позже всех остальных работ сети в завершающем событии.
 ;
;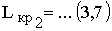 .
. , предшествующую (6,7). Код этой работы должен оканчиваться на 6. Таких работ две – (4,6) и (3,6). Но только одна из них, работа (3,6) по времени своего окончания вплотную "примыкает" на графике к началу работы (6,7). Допишем слева найденную критическую работу (3,6) к выражению (2.1)
, предшествующую (6,7). Код этой работы должен оканчиваться на 6. Таких работ две – (4,6) и (3,6). Но только одна из них, работа (3,6) по времени своего окончания вплотную "примыкает" на графике к началу работы (6,7). Допишем слева найденную критическую работу (3,6) к выражению (2.1) .
. .
. .
. приводит к результату
приводит к результату  .
.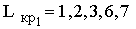 и
и  .
.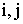
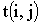


 дней). Поскольку (5,7) завершающая работа сети, то ее полный и свободный резервы равны
дней). Поскольку (5,7) завершающая работа сети, то ее полный и свободный резервы равны  .
. .
. .
. . Но если сдвинуть во времени работу (4,5) на 1 день, то работа (5,7) также сдвинется на 1 день и это не нарушит срок выполнения проекта, т.к. у работы (5,7) есть временной резерв. Таким образом согласно правилу №2.1
. Но если сдвинуть во времени работу (4,5) на 1 день, то работа (5,7) также сдвинется на 1 день и это не нарушит срок выполнения проекта, т.к. у работы (5,7) есть временной резерв. Таким образом согласно правилу №2.1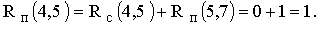
 . Кроме того, поскольку последующая работа (5,7) имеет резерв в 1 день, то, в общем, работу (1,5) можно сдвинуть на 3 дня и это не нарушит сроков проекта (см. рис.2.4), т.е.
. Кроме того, поскольку последующая работа (5,7) имеет резерв в 1 день, то, в общем, работу (1,5) можно сдвинуть на 3 дня и это не нарушит сроков проекта (см. рис.2.4), т.е.
 . Поскольку после работы (1,4) следуют две работы с различными полными резервами, то согласно правилу №2.1
. Поскольку после работы (1,4) следуют две работы с различными полными резервами, то согласно правилу №2.1
 . Поскольку обе последующие работы критические, то полный и свободный резерв работы (1,3) совпадают
. Поскольку обе последующие работы критические, то полный и свободный резерв работы (1,3) совпадают

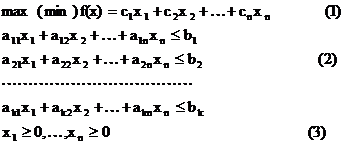
 (точку максимума), чтобы:
(точку максимума), чтобы: