Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение потока заданной величины минимальной стоимости. Алгоритмы Басакера-Гоуэна, КлейнаВ предыдущем разделе рассматривалась сеть Для данной задачи нахождения потока заданной величины минимальной стоимости необходимо, каждой дуге
Постановка задачи. Пусть При этом подразумевается, что величина В излагаемых далее алгоритмах построения потока минимальной стоимости существенную роль играет так называемый граф модифицированных стоимостей Пусть дан граф a) Если b) Если c) Если
Пример. Пусть задан граф В данном графе над каждой дугой 
Рис. 1.22
Рис. 1.23
Алгоритм Басакера-Гоуэна (Basaker R.G., Gowen P.J)
Шаг 0. Решение начинаем с нулевого потока Шаг 1. Строим граф модифицированных стоимостей Шаг 3. В исходном графе определяем
на обратных:
Находим На прямых дугах пути P величину потока увеличиваем, а на обратных уменьшаем на Шаг 4 Полагаем Если
Замечание. Для решения задачи о нахождении максимального потока максимальной стоимости достаточно в алгоритме Басакера-Гоуэна заменить
Пример.Построить поток заданной мощности Итерация 1 Полагаем Находим кратчайшую (наиболее дешевую) цепь P* из s в t: P*: s " b " a " t, Длина цепи (модифицированная стоимость) равна 3. Соответствующий ей (s, t) – путь P: s " b " a " t, и Т.к. все дуги пути — прямые, то увеличивая пути P величину потока на 2, то получаем (см. Рис. 1.26)
Рис. 1.24
Рис. 1.25
Рис. 1.26 Пересчитываем Поскольку
Итерация 2 Стром граф модифицированных стоимостей
Рис. 1.27
Находим в графе модифицированных стоимостей кратчайшую цепь P*: s " a " b " t, Соответствующий ей (s, t) – путь P: s " a На прямых дугах пути P вычисляем:
на обратных:
Находим Величину потока на прямых дугах (s, a), (b, t) увеличиваем, а на обратной (a, b) уменьшаем на 1. Получаем (см. Рис. 1.28)
Рис. 1.28 Считаем Т.к. Вычислим суммарную стоимость пропущенного потока: S(f)=1*5+1*2+1*1+1*2+6*1=16.
Очевидно, что при достаточно больших значениях Следующий алгоритм, предложенный Клейном, позволяет эти вычисления сократить.
Алгоритм Клейна (Klein M.)
Шаг 0.Решение начинаем с любого потока f из источника в сток мощности
Шаг 1. Строим граф модифицированных стоимостей Шаг 2. Находим в графе Шаг 3. В исходной сети G определяем замкнутый путь P, соответствующий циклу P*. Прямыми дугами в этом цикле считаем дуги сонаправленные соответствующим дугам цикла P* в графе
на обратных: Находим На прямых дугах пути P величину потока увеличиваем, а на обратных уменьшаем на Шаг 4. Пересчитываем Пример.Построить поток заданной мощности В сети построен поток мощности Итерация 1 Находим Находим цикл отрицательной длины P* (можно воспользоваться алгоритмом Флойда): P*: b " t " c " b,
Рис. 1.29
Рис. 1.30
Рис. 1.31 Длина цикла На прямых дугах пути P((b, t), (c, b)) вычисляем:
На обратной (t, c)
Находим Величину потока на прямых дугах увеличиваем, а на обратной — уменьшаем на 2. Получаем: (см. рис. 1.32)
Рис. 1.32
Находим стоимость нового потока:
Итерация 2 Строим граф модифицированных стоимостей
Рис. 1.33 В построенном графе отсутствуют циклы отрицательной длины. Упражнение: Доказать этот факт при помощи алгоритма Флойда. Т.о., в данной сети построен оптимальный поток, его стоимость равна 27.
Очевидно, что оба рассмотренных алгоритма позволяют найти поток мощность
Теорема.Поток величины
Упражнения a) Пусть b) Пусть задана сеть, в которой мощность максимального потока равна - Пусть известно, что мощность максимального потока в сети должна быть равной - Пусть известно, что суммарные затраты на пропущенный в сети поток не должны превышать заданной величины S. Как следует увеличить пропускные способности дуг, чтобы в преобразованной сети можно было бы пропустить поток как можно большей мощности? c) В задаче о потоке минимальной стоимости поток является оптимальным тогда и только тогда, когда в графе модифицированных стоимостей не существует отрицательных циклов. Объяснить, почему при поиске максимального потока минимальной стоимости, граф можно разбить на две части и в каждой из них отдельно искать отрицательные циклы.
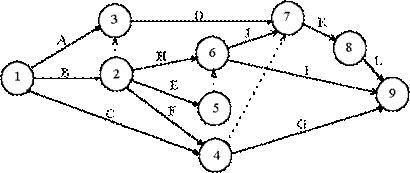
Сетевое планирование Построение сетевых моделей Построение сетевой модели (структурное планирование) начинается с разбиения проекта на четко определенные работы, для которых определяется продолжительность. Работа – это некоторый процесс, приводящий к достижению определенного результата, требующий затрат каких-либо ресурсов и имеющий протяженность во времени. По количеству затрачиваемого времени работа может быть: - действительной, т.е. требующей затрат времени; - фиктивной, т.е. формально не требующей затрат времени. Фиктивная работа может реально существовать, например, "передача документов от одного отдела к другому". Если продолжительность такой работы несоизмеримо мала по сравнению с продолжительностью других работ проекта, то формально ее принимают равной 0. Существуют фиктивные работы, которым в реальности не соответствуют никакие действия. Такие фиктивные работы только представляют связь между другими работами сетевой модели. Работы связаны друг с другом таким образом, что выполнение одних работ может быть начато только после завершения некоторых других. Событие – это момент времени, когда завершаются одни работы и начинаются другие. Событие представляет собой результат проведенных работ и, в отличие от работ, не имеет протяженности во времени. Взаимосвязь работ и событий, необходимых для достижения конечной цели проекта, изображается с помощью сетевого графика (сетевой модели). Работы изображаются стрелками, которые соединяют вершины, изображающие события. Начало и окончание любой работы описываются парой событий, которые называются начальным и конечным событиями. Поэтому для указания конкретной работы используют код работы (i, j), состоящий из номеров начального (i-го) и конечного (j-го) событий (рис.2.1).
Рис.2.1. Кодирование работы Любое событие может считаться наступившим только тогда, когда закончатся все входящие в него работы. Поэтому работы, выходящие из некоторого события, не могут начаться, пока не будут завершены все работы, входящие в это событие. Событие, не имеющее предшествующих ему событий, т.е. с которого начинается проект, называют исходным. Событие, которое не имеет последующих событий и отражает конечную цель проекта, называется завершающим. При построении сетевого графика необходимо следовать следующим правилам: 1. длина стрелки не зависит от времени выполнения работы; 2. стрелка может не быть прямолинейным отрезком; для действительных работ используются сплошные, а для фиктивных – пунктирные стрелки; 3. каждая операция должна быть представлена только одной стрелкой; 4. между одними и теми же событиями не должно быть параллельных работ, т.е. работ с одинаковыми кодами; 5. следует избегать пересечения стрелок; 6. не должно быть стрелок, направленных справа налево; 7. номер начального события должен быть меньше номера конечного события; 8. не должно быть висячих событий (т.е. не имеющих предшествующих событий), кроме исходного; 9. не должно быть тупиковых событий (т.е. не имеющих последующих событий), кроме завершающего; 10. не должно быть циклов (рис.2.2).
Рис.2.2. Недопустимость циклов Исходные данные для построения сетевой модели могут задаваться различными способами, например, - описанием предполагаемого проекта. В этом случае необходимо самостоятельно разбить его на отдельные работы и установить их взаимные связи; - списком работ проекта. В этом случае необходимо проанализировать содержание работ и установить существующие между ними связи; - списком работ проекта с указанием их упорядочения. В этом случае необходимо только отобразить работы на сетевом графике. Построение сетевого графика необходимо начинать с выявления исходных работ модели. Если согласно условию некоторая работа может выполняться, не ожидая окончания каких-либо других работ, то такая работа является исходной в сетевой модели и ее начальным событием является исходное событие. Если исходных работ несколько, то их стрелки выходят все из одного исходного события. Если, согласно условию, после окончания некоторой работы не должны выполняться никакие другие работы, то такая работа является завершающей работой сетевой модели и ее конечным событием является завершающее событие. Если завершающих исходных работ несколько, то их стрелки заходят все в одно завершающее событие. Если, согласно условию, несколько работ имеют общее начальное и общее конечное события, то они являются параллельными, имеют одинаковый код, что недопустимо. Для устранения параллельности работ вводят дополнительное событие и фиктивную работу (которой в реальности не соответствует никакое действие) таким образом, чтобы конечные события работ различались (рис.2.3.).
Рис.2.3. Устранение параллельности двух работ Пример 1. Постройте сетевую модель программы опроса общественного мнения, которая включает разработку (A; 1 день) и распечатку анкет (B; 0,5 дня), прием на работу (C; 2 дня) и обучение (D; 2 дня) персонала, выбор опрашиваемых лиц (E; 2 дня), рассылку им анкет (F; 1 день) и анализ полученных данных (G; 5 дней). Решение: Из условия задачи нам известно содержание работ, но явно не указаны взаимосвязи между работами. Поэтому для их установления необходимо проанализировать смысл каждой конкретной работы и выяснить, какие из остальных работ должны ей непосредственно предшествовать. Исходной работой, начинающей сетевой график, в данном случае является "прием на работу" (С), поскольку все остальные работы должны выполняться уже принятыми на работу сотрудниками (рис.7.4). Перед выполнением всех работ по опросу общественного мнения сотрудников необходимо обучить персонал (D). Перед тем как разослать анкеты (F), их надо разработать (A), распечатать (B) и выбрать опрашиваемых лиц (E), причем работу с анкетами и выбор лиц можно выполнять одновременно. Завершающей работой проекта является анализ полученных данных (G), который нельзя выполнить без предварительной рассылки анкет (F). В результате этих рассуждений построим сетевую модель и пронумеруем события модели (см. рис.2.4).
Рис.2.4. Сетевая модель программы опроса общественного мнения Пример 2. Постройте сетевую модель, включающую работы A, B, C, ..., L, которая отображает следующее упорядочение работ: 1) A, B и C – исходные операции проекта; 2) A и B предшествуют D; 3) B предшествует E, F и H; 4) F и C предшествует G; 5) E и H предшествуют I и J; 6) C, D, F и J предшествуют K; 7) K предшествует L. Решение: В пункте 1) условия явно указано, что A, B и C являются исходными работами, поэтому изобразим их тремя стрелками, выходящими из исходного события 1. Пункт 2) условия означает, что стрелки работ A и B должны окончиться в одном событии, из которого выйдет стрелка работы D. Но поскольку стрелки работ A и B также и начинаются в одном событии, то имеет место параллельность работ, которая недопустима правилами построения сетевых моделей (см. рис.2.5).
Рис.2..5. Устранение параллельности работ A и B Для ее устранения введем дополнительное событие 2, в которое войдет работа B, после чего соединим события 2 и 3, в которые входят работы A и B пунктирной стрелкой фиктивной работы. В данном случае фиктивная работа (2,3) не соответствует никакой реальной работе, а лишь отображает логическую связь между работами B и D. Дальнейшее построение рассмотрим с помощью рис.2.6
Рис.2.6. Сетевая модель примера 2 Согласно пункту 3) условия задачи из события 2, выходят три стрелки работ E, F и H. Согласно пункту 4) условия задачи стрелки работ C и F должны войти в общее событие, из которого выйдет стрелка работы G. Проблема с параллельностью работ E и H [пункт 5) условия задачи] решается путем введения дополнительного события 5 и фиктивной работы (5,6). Для отображения в сетевой модели пункта 6) условия задачи введем стрелки работ D и J в событие 7, а связь работ F и C с работой K отобразим с помощью фиктивной работы (4,7). Стрелки работ F и C нельзя было напрямую вводить в событие 7, потому что после них должна следовать работа G, которая с работами D и J никак не связана. Стрелка работы L выходит из события 8, т.е. после окончания работы K в соответствии с пунктом 7) условия задачи. Поскольку в условии не указано, что работы L, I и G предшествуют каким-либо другим работам, то эти работы являются завершающими и их стрелки войдут в завершающее событие 9. Нумерацию событий проводят после построения сетевого графика, следя за тем, чтобы номер начального события каждой работы был меньше номера ее конечного события.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 2074. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , каждой дуге (x, y) которой соответствовала пропускная способность дуги
, каждой дуге (x, y) которой соответствовала пропускная способность дуги  , указывающая максимальное количество потока, которое по ней можно пропустить.
, указывающая максимальное количество потока, которое по ней можно пропустить. было поставлено в соответствие неотрицательное действительное число
было поставлено в соответствие неотрицательное действительное число  , называемое стоимостью доставки единицы потока по дуге
, называемое стоимостью доставки единицы потока по дуге  .
. и стоимостями
и стоимостями  ,
,  ) заданной мощности
) заданной мощности  , найти поток минимальной стоимости
, найти поток минимальной стоимости  .
. не превышает максимальной мощности допустимого потока из s в t, иначе задача не имеет решения.
не превышает максимальной мощности допустимого потока из s в t, иначе задача не имеет решения. .
. строится следующим образом: множество вершин совпадает с множеством вершин графа G, т.е.
строится следующим образом: множество вершин совпадает с множеством вершин графа G, т.е.  ; множество
; множество  определяется правилами:
определяется правилами: , то в графе
, то в графе  , имеющая длину (модифицированную стоимость)
, имеющая длину (модифицированную стоимость) 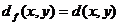 .
. , то в графе
, то в графе  , имеющая длину (модифицированную стоимость)
, имеющая длину (модифицированную стоимость)  .
.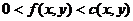 , то в графе
, то в графе 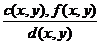 показывают соответственно пропускную способность, пропущенный по дуге поток и стоимость единицы потока. Тогда граф
показывают соответственно пропускную способность, пропущенный по дуге поток и стоимость единицы потока. Тогда граф 

 . Полагаем
. Полагаем 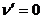 .
.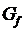 нет ни одной цепи из s в t, то задача нахождения потока минимальной стоимости, имеющего заданную мощность,
нет ни одной цепи из s в t, то задача нахождения потока минимальной стоимости, имеющего заданную мощность,  минимальной стоимости. В противном случае находим кратчайшую цепь
минимальной стоимости. В противном случае находим кратчайшую цепь  из s в t (роль длин дуг играют их модифицированные стоимости).
из s в t (роль длин дуг играют их модифицированные стоимости).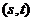 - путь P, соответствующий цепи P*. На прямых дугах пути P вычисляем:
- путь P, соответствующий цепи P*. На прямых дугах пути P вычисляем:
 .
. .
.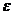 .
. .
. , то переходим к шагу 1, если
, то переходим к шагу 1, если 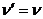 , то алгоритм свою работу закончил, в сети построен оптимальный поток.
, то алгоритм свою работу закончил, в сети построен оптимальный поток. .
. (см. Рис. 1.24).
(см. Рис. 1.24). (см. Рис. 1.25).
(см. Рис. 1.25). .
.


 .
. , то переходим к шагу 1.
, то переходим к шагу 1.
 b " t.
b " t. ,
, .
. .
.
 .
.
 . Если в графе модифицированных стоимостей
. Если в графе модифицированных стоимостей  мощности
мощности  .
. и переходим к шагу 1.
и переходим к шагу 1. =1*3+2*3+2*3+3*2+8*2=37. Строим граф модифицированных стоимостей
=1*3+2*3+2*3+3*2+8*2=37. Строим граф модифицированных стоимостей 


 . Соответствующий ему путь в сети G: P: b " t
. Соответствующий ему путь в сети G: P: b " t 
 .
.
 .
.
 — сеть, с заданными пропускными способностями
— сеть, с заданными пропускными способностями  ,
, 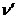 ,
,  . Каким образом следует увеличить пропускные способности дуг, чтобы получить необходимый поток с минимальными затратами (то есть с минимальным увеличением стоимости потока)?
. Каким образом следует увеличить пропускные способности дуг, чтобы получить необходимый поток с минимальными затратами (то есть с минимальным увеличением стоимости потока)?