
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Построение потоков максимальной мощности. Алгоритм Форда-ФалкерсонаОпределение Ориентированный граф G = (V, E) называется сетью, если в нем отмечены (выделены) некоторые вершины, называемые полюсами; при этом, множество полюсов разбито на два подмножества: вершины первого подмножества являются источниками, а второго — стоками. Остальные вершины называются внутренними. В данном разделе рассматриваются только сети, где имеется один источник s (sourse) и один сток t (target). Для каждой вершины
E+( ν) = {( ν, u) E-( ν) = {( u, ν)
Пусть f: E " R – некоторая функция на дугах. Дивергенцией f в вершине ν называется число
Функция f: E " R называется потоком в сети, если во всех внутренних вершинах выполнено равенство div f (ν) = 0. Данное условие называется условием неразрывности. Оно означает (если интерпретировать f(e) как количество жидкости, протекающей по дуге в единицу времени), что для любой внутренней вершины ν количество жидкости, втекающей в эту вершину, равно количеству жидкости, вытекающей из нее. Пример. Пусть задан граф G=(V, E), в котором пропущен допустимый поток f (рис.1.16).
Рис. 1.16
Числа c(x, y), f(x, y), стоящие над дугой (x, y) графа, показывают соответственно пропускную способность и пропущенный поток в этой дуге. Очевидно, что, например, во внутренних вершинах сети a и b дивергенция равна нулю, т.е. выполняется условие неразрывности, или, по-другому, в сети задан поток.
Определение Мощностью потока называется число
M(f) = div f(s) = - div f(t). M(f) интерпретируется как количество жидкости «создаваемое» источником и, соответственно, равное (в силу неразрывности) количеству жидкости «потребляемому» стоком. В приведенном примере мощность потока равна 4.  Пусть каждой дуге 0<= f(e)<= c(e) для любой дуги e Т.к. в дуге (s, a) (рис. 4.1) пропускная способность равна двум единицам, то в ней задан допустимый поток, который также равен двум единицам. Постановка задачи. Задана сеть с фиксированными пропускными способностями дуг. Найти среди допустимых потоков поток максимальной мощности. В связи с излагаемым ниже алгоритмом решения этой задачи, потребуется рассмотреть еще ряд объектов, ассоциированных с сетями и потоками. Пусть Для разреза (X, X*) введем множество E+(X, X*) = {e(u, ν) дуг, идущих из X в X*. Определение Пропускной способностью разреза (X, X*) называется число
В приведенном выше примере, рассмотрим, например, разрез (X, X*) с множествами X={s, a} и X*={b, t}. Видим, что его мощность равна C(X, X*) = c(s, b)+c(a, b) +с(a, t)=3+1+4=8. Теорема(Ford-Fulkerson).(Необходимое условие максимального потока). Если f – допустимый поток максимальной мощности, то существует разрез (X, X*), такой что M(f)=C(X, X*). Пусть s"t – некоторый путь (без учета ориентации), т.е. последовательность вершин s = ν0, ν1,…, νk = t такая, что для любого i=0,…,k-1 либо (νi, νi+1) Например, на рис. 4.2 показаны, какие дуги являются прямыми, а какие обратными.
Дуги (s, ν1), (ν3, ν4), (ν4, t) – прямые, а дуги (ν2, ν1), и (ν3, ν2) - обратные. Пусть f – некоторый допустимый поток. Тогда путь s" t является увеличивающим для f, если на каждой прямой дуге e:f(e)<c(e), а на каждой обратной дуге e:f(e)>c(e).Для такого пути вычисляют для прямых дуг
Очевидно, что изменяя исходный поток f (вдоль пути s" t) на прямых дугах на величину (+
В заданной сети построен максимальный поток тогда и только тогда, когда не существует ни одного увеличивающего пути. Алгоритм Форда-Фалкерсона Шаг 0. Пропускаем по сети некоторый допустимый поток (возможно нулевой). В процессе работы алгоритма (на каждом этапе) каждая вершина относится к одному из трех множеств: - непомеченные вершины, - помеченные, но не просмотренные, (окрашенные). - просмотренные (окрашенные). Шаг 1. Пометим вершину S меткой (S+, Шаг 2. Пусть a) b) В обоих случаях a) и b) помечаем вершину u меткой и вносим в множество помеченных, но не просмотренных вершин.
c) Если Когда все соседние с Шаг 3. Повторяем шаг 2 (т.е. расширяем просмотренное множество) до тех пор, пока не возникнет одна из следующих ситуаций: a)Все вершины графа разбиты на два подмножества: - просмотренные (окрашенные); - непомеченные вершины, включающие в себя и вершину t. Тогда в сети построен максимальный поток мощности V и минимальный разрез (X, X*), где X – окрашенные вершины. b) Если вершина T получила метку, то в сети существует увеличивающий путь s" t, который можно определить, идя из t обратно назад к s. Т.е. если метка у t была Мощность потока увеличилась на Переходим опять к шагу 1. При этом множество X окрашенных вершин задает разрез (X, X*) пропускная способность которого равна мощности потока.
Пример. Для сети с заданными пропускными способностями дуг (рис. 1.17) необходимо построить поток максимальной мощности и указать разрез (X, X*) для которого M(f)=C(X, X*). Решение На первом шаге помечается узел S (S+, Шаг 1. Рассмотрим узлы, соседние с S. Узел a помечается меткой (S+,3), т.к. (s, a) – дуга, f(s, a)=2<c(s, a)=5 и min( Узел b помечается меткой (S+,1), т.к. (s, b) – дуга, f(s, b)=3<c(s, b)=4 и min( Узел d не помечается, т.к. (s, d) – дуга и f(s, d)=4=c(c, d). Данный узел отнесем к множеству просмотренных узлов (рис. 1.18).
Рис. 1.17

Рис. 1.18 Шаг 2. Рассмотрим непомеченный узел t, соседний с помеченным и не просмотренным узлом a. Узел t не помечается, т.к. (a, t) – дуга и f(a, t)=2=c(a,t). Узел a после этого отнесем к множеству просмотренных узлов Шаг 3. Рассмотрим непомеченные узлы, соседние с узлом b. Узел t не помечается, т.к. f(b, t) = 4 = c(b,t). Узел d получает пометку (b-, 1), т.к (d, b) – дуга и f(d, b)=1>0 и min(
Рис. 1.19
Шаг 4. Узел t получает метку (d+, 1), поскольку является соседним с помеченным и не просмотренным узлом d, (d, t) – дуга, и f(d, t) = 3< c(d, t) = 5 и Т.к. xt=d+, xd=b-, xb=s+, то P(s, b, d, t). На прямых дугах (s, b) и (d, t) этого пути увеличиваем поток на
Рис. 1.20 Необходимо снова увеличить поток. Пометим узел S(s+, Рассмотрим непомеченные узлы, соседние с узлом a. Узел t не помечается, т.к. (a, t) – дуга и f(a, t)=2=c(a, t). Узел b не помечается, т.к. (b, a) – дуга и f(b, a)=0. Узел a переходит в множество просмотренных узлов. Поскольку в сети нет помеченных и не просмотренных узлов, то полученный поток является максимальным. Определим минимальный разрез. К множеству X относятся все помеченные узлы: X = {s, a}, к
Величина потока V=10 равна суммарной пропускной способности дуг разреза.
Рис. 1.21
Обобщенные задачи о потоке Рассмотрим некоторые обобщения задачи о нахождении максимального потока заданной сети, которые также могут быть решены с помощью рассматриваемого базового алгоритма Форда-Фалкерсона.
|
||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 738. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 выделим два множества дуг:
выделим два множества дуг: E} выходящих из ν, и
E} выходящих из ν, и

 поставлено в соответствие некоторое число c(e) >=0, называемое пропускной способностью дуги. Поток f является допустимым, если выполняется условие:
поставлено в соответствие некоторое число c(e) >=0, называемое пропускной способностью дуги. Поток f является допустимым, если выполняется условие: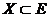 — некоторое подмножество вершин, удовлетворяющих условию
— некоторое подмножество вершин, удовлетворяющих условию  Пара (X, X*), где X* = V \ X называется разрезом, отделяющим вершину s от вершины t.
Пара (X, X*), где X* = V \ X называется разрезом, отделяющим вершину s от вершины t.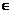 E: u
E: u 

 по формуле:
по формуле: , а для обратных дуг —
, а для обратных дуг —  :
: . Затем вычисляют
. Затем вычисляют  .
.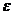 ) и на обратных дугах на величину (-
) и на обратных дугах на величину (- 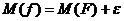
 ). Остальные вершины не помечены, S помеченная, но не просмотрена.
). Остальные вершины не помечены, S помеченная, но не просмотрена. — некоторая помеченная, но не просмотренная вершина с пометкой. Рассмотрим все соседние с
— некоторая помеченная, но не просмотренная вершина с пометкой. Рассмотрим все соседние с  и
и 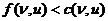 , тогда вершина u получает метку (
, тогда вершина u получает метку ( 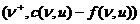 .
. и
и  , тогда u получает метку
, тогда u получает метку  .
.
 , то u не помечается.
, то u не помечается. , то соединяем t с ν1 и т.д. Для найденного пути определяем величину
, то соединяем t с ν1 и т.д. Для найденного пути определяем величину 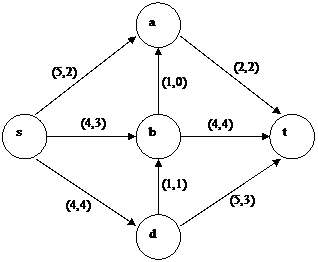
 =1, f(d, b)=1). Узел b переходит к множеству просмотренных узлов (рис. 1.19).
=1, f(d, b)=1). Узел b переходит к множеству просмотренных узлов (рис. 1.19).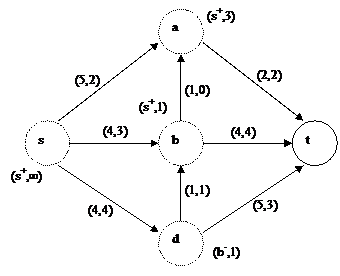
 = 1= min(1, 5-3). Определим путь P, увеличивающий поток.
= 1= min(1, 5-3). Определим путь P, увеличивающий поток.
 = {b, d, t}. В разрез входят дуги, идущие из узлов множества X в узлы множества
= {b, d, t}. В разрез входят дуги, идущие из узлов множества X в узлы множества 